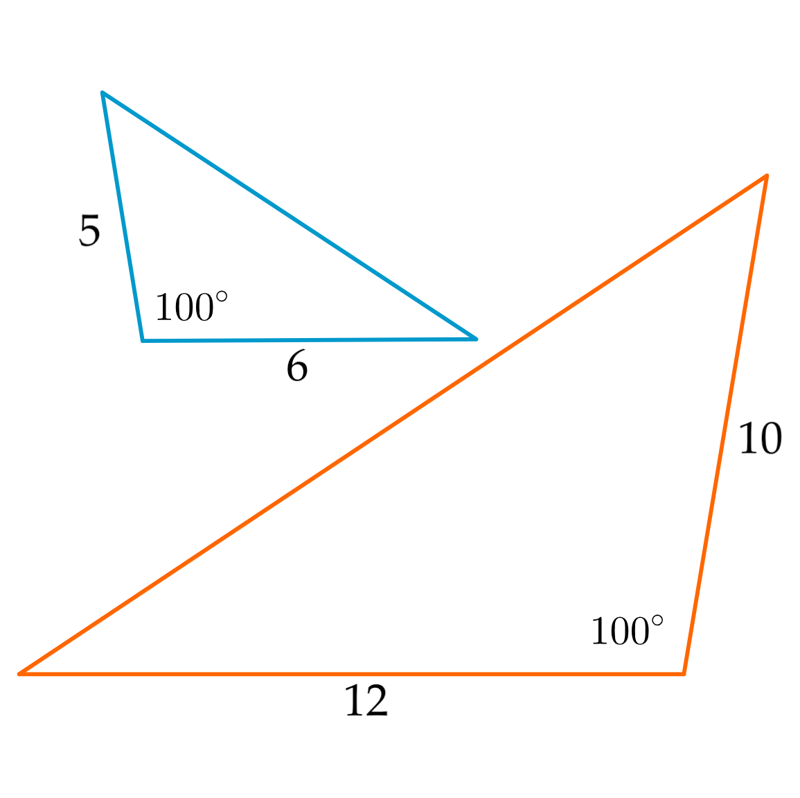Valemid ja reeglid

More like this

Aritmeetika

Tehted ratsionaalarvudega

Liitmine ja lahutamine

Reegel

-a-b=-\left(a+b\right)

-b+a=a-b

a-\left(-b\right)=a+b

Näide

–5 – 7 = –(5 + 7) = –12

–5 + 7 = 7 – 5 = 2

5 – (–7) = 5 + 7 = 12

Korrutamine

Reegel

-a\cdot\left(-b\right)=a\cdot b

a\cdot\left(-b\right)=-a\cdot b

0\cdot a=0

Näide

–5 ⋅ (–7) = 35

5 ⋅ (–7) = –35

0 ⋅ 5 = 0

Jagamine

Reegel

-a\ :\ \left(-b\right)=\frac{a}{b}

a\ :\ \left(-b\right)=-\frac{a}{b}

-a\ :\ b=-\frac{a}{b}

Näide

-12\ :\ \left(-3\right)=\frac{12}{3}=4

12\ :\ \left(-3\right)=-\frac{12}{3}=-4

-12\ :\ 3=-\frac{12}{3}=-4

Nulli jagatises

Reegel

0\ :\ a\ =\ 0

Nulliga ei saa jagada!

Näide

0\ :\ 12\ =\frac{0}{12}=0

NB! a ja b on positiivsed arvud.

Korda reeglit

6 – 9 =
–6 + 9 =
9 + 6 =
–9 – 6 =
–6 + 0 =

4 ⋅ (–6) =
–8 ⋅ (–7) =
–9 ⋅ (+3) =
2 ⋅ 0 ⋅ (–3) =
+5 ⋅ 8 =

28 : (–7) =
–63 : (–9) =
45 : 5 =
0 : (–1) =
12 : 0 =

Vastandarv ja absoluutväärtus

Vastandarv

Reegel

Arvu a vastandarv on –a.

-\left(-a\right)=a

a+\left(-a\right)=0

Näide

Arvu 7 vastandarv on –7.

–(–9) = 9

7 + (–7) = 0

Absoluutväärtus

Reegel

\left|a\right|=a

\left|-a\right|=a

\left|0\right|=0

Näide

\left|13\right|=13

\left|-13\right|=13

Järjestamine

Reegel

Kui \left|b\right|>\left|a\right|, siis b>a

Kui \left|-b\right|<\left|-a\right|, siis -b>-a

Näide

\left|9\right|>\left|8\right|

\left|-4\right|<\left|-9\right|,\ -4>-9

NB! a ja b on positiivsed arvud.

Korda reeglit

–10
–7
–5
–3
3
5
7
10

Arv a	–a	\|a\|
5
	10
–3
	–7

–5 |–5|
3 |–3|
|–6| |4|
–(–4) –4
–|5| –3

Märka sümboleid

∈ ∉	kuulub hulkaei kuulu hulka
=≠	võrdneei ole võrdne
≈	ümardatud tulemus
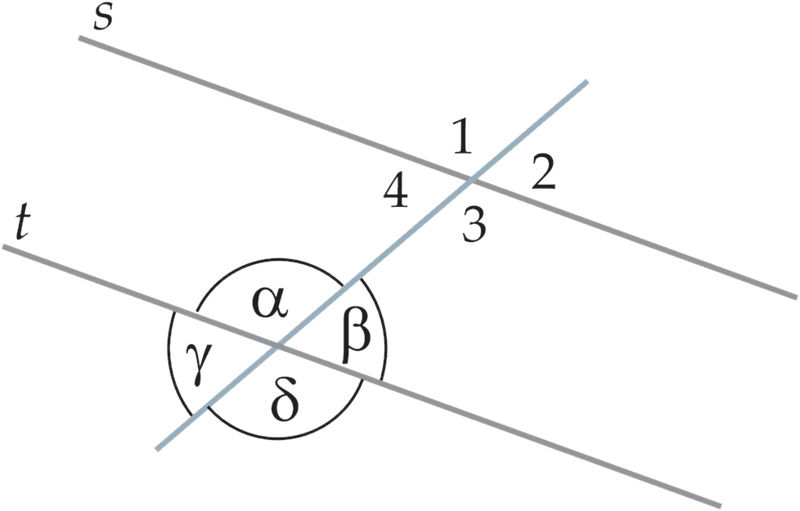
‖\nparallel	paralleelneei ole paralleelne
⊥	ristumine
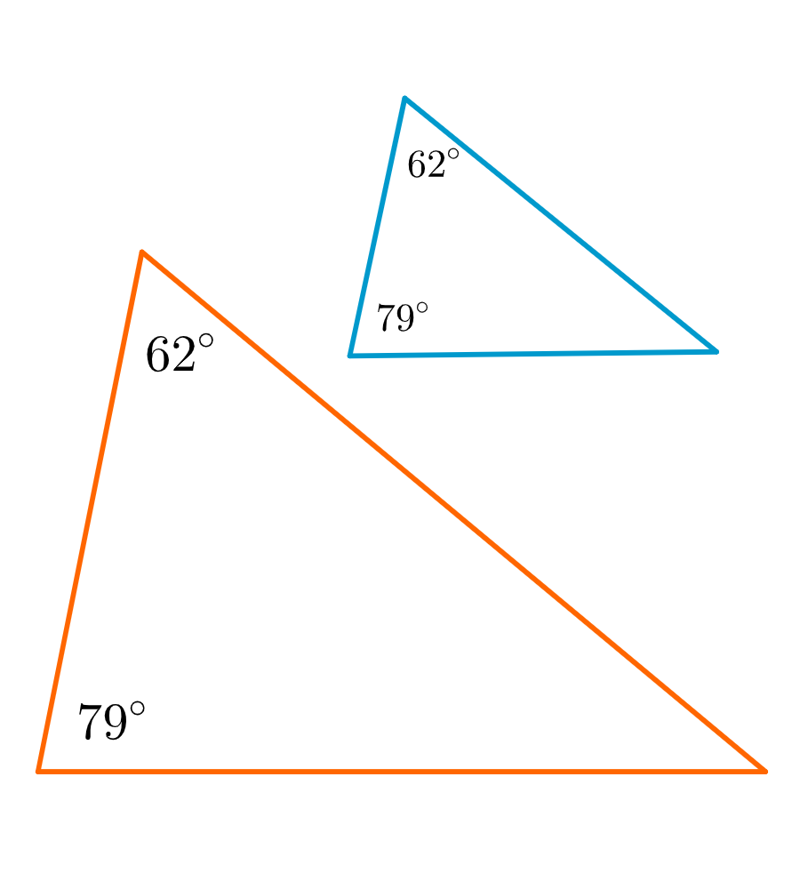
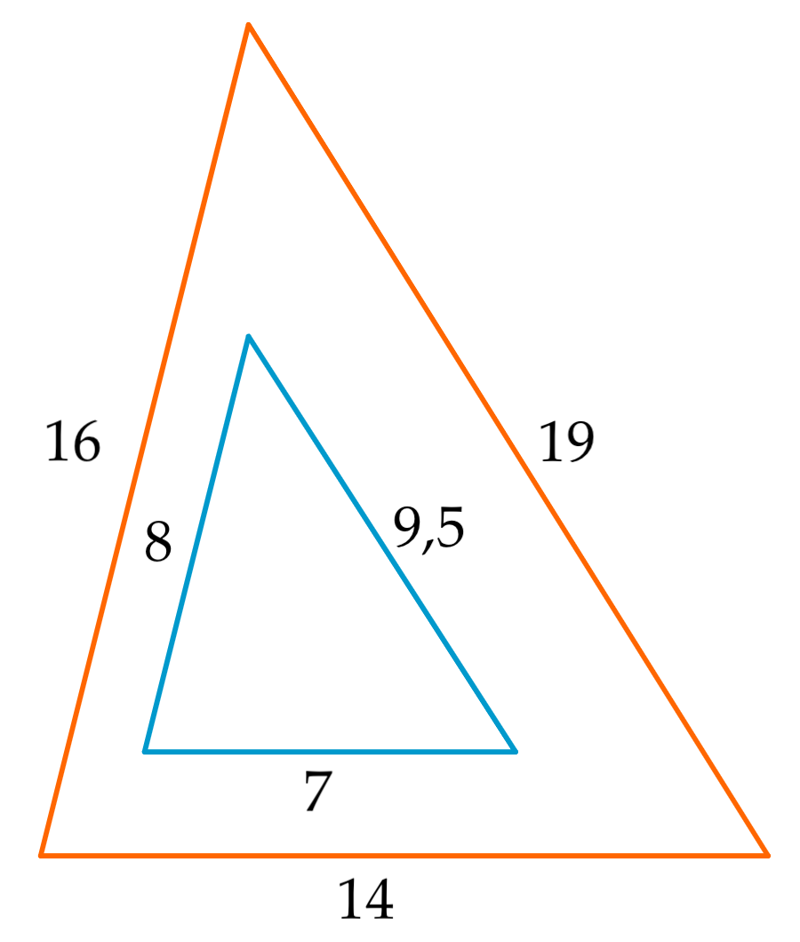
∼	sarnased kujundid
A ⇒ B	A-st järeldub B

More like this

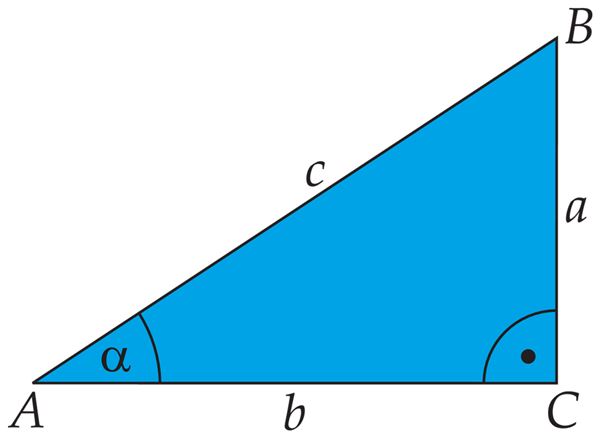
Kiirus, aeg, teepikkus

Ühtlane liikumine

Teepikkus

s=v\cdot t

Kiirus

v=\frac{s}{t}

Aeg

t=\frac{s}{v}

Teisendamine

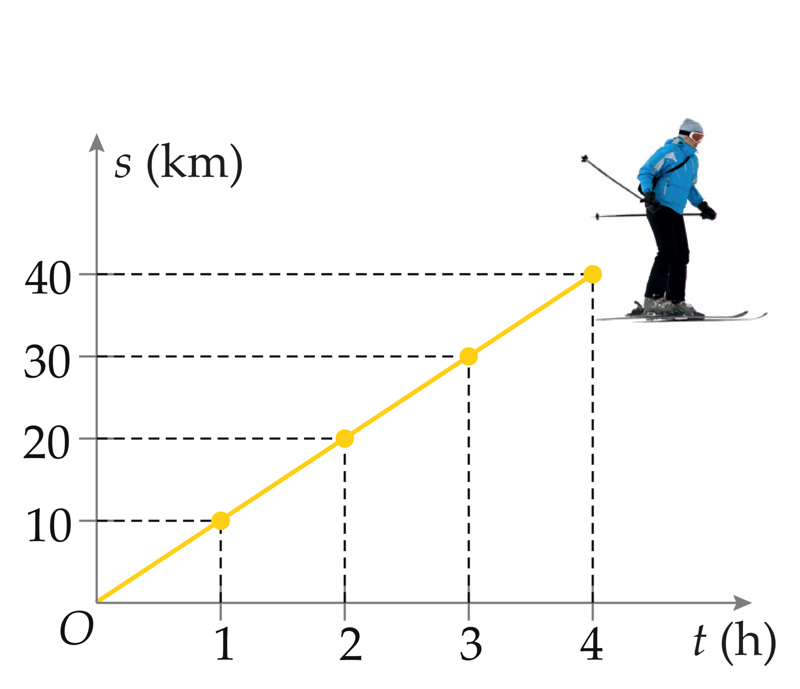
1\frac{\mathrm{m}}{\mathrm{s}}=3,6\frac{\mathrm{km}}{\mathrm{h}}

Nelja tunniga liigub suusataja km.
Kui suusatatud on 25 km, siis on suusataja liikunud tundi.
Suusataja keskmine kiirus on \frac{\mathrm{km}}{\mathrm{h}}.
Tartu maratoni läbimiseks (63 km) kuluks suusatajal sellise kiirusega sõites

mitte rohkem kui 7 tundi
alla 5 tunni
peaaegu 10 tundi
üle 12 tunni

More like this

Protsent

Mis on protsent?

1\%=\frac{1}{100}=0,01

p\%=\frac{p}{100}=0,01p

Mis on osa ja osamäär?

\mathrm{osamäär=\frac{\mathrm{osa}}{tervik}}

\mathrm{osa=osamäär\ \cdot\ tervik}

Mis on promill?

1‰=\frac{1}{1000}=0,001

Sõber soovitab

Märka protsenti

1%	\frac{1}{100}	sajandik	0,01
5%	\frac{1}{20}	kahekümnendik	0,05
10%	\frac{1}{10}	kümnendik	0,1
20%	\frac{1}{5}	viiendik	0,2
25%	\frac{1}{4}	veerand	0,25
50%	\frac{1}{2}	pool	0,5
75%	\frac{3}{4}	kolmveerand	0,75
100%	1	tervik	1
150%	1\frac{1}{2}	poolteist	1,5

Korda reeglit

1
2
5
10
15
50

1% arvust 500 on
10% arvust 100 on
20% arvust 50 on
25% arvust 200 on
50% arvust 20 on
200% arvust 0,5 on

1%
5%
10%
20%
25%
50%
200%

2 on 4-st
10 on 200-st
9 on 36-st
44 on 22-st
5 on 25-st
10 on 1000-st

More like this

Algebra

Tehted astemetega

a^m\cdot a^n=a^{m+n}

a^m\ :\ a^n=a^{m-n}

\left(a^m\right)^n=a^{m\cdot n}

\left(a\cdot b\right)^m=a^m\cdot b^n

\left(\frac{a}{b}\right)^m=\frac{a^m}{b^n},\ b\ne0

a^0=1,\ a\ne0

\sqrt{b}=a ⇒ a^2=b,\ b\ge0Nulliga ei saa jagada!

0
1
2
$2^{4}$
$2^{5}$
$2^{6}$

2^3\cdot2^2= 2^8\ :\ 2^2\ =\ \left(2^3\right)^2= 2^0= \left(10\ :\ 5\right)^4= \left(4\cdot0,5\right)^5=

Abivalemid

\left(a+b\right)^2=a^2+2ab+b^2

\left(a-b\right)^2=a^2-2ab+b^2

\left(a-b\right)\left(a+b\right)=a^2-b^2

\left(a-b\right)^2=\left(b-a\right)^2

\left(-a-b\right)^2=\left(a+b\right)^2

a\left(b+c\right)=ab+ac

\left(a+b\right)\left(c+d\right)=ac+ad+bc+bd

\left(a+b\right)\ :\ c=a\ :\ c+b\ :\ c=\frac{a}{c}+\frac{b}{c}

\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}

Korda reeglit

$x^{2} - 9$
$x^{2} + 9$
$x^{2} - 6 x + 9$
$x^{2} + 6 x + 9$

\left(x+3\right)^2=
\left(x-3\right)^2=
\left(x-3\right)\left(x+3\right)=
\left(3-x\right)^2=

$2 x - 1$
$2 x$
$x^{2} + 2$
$x^{2} + x - 6$
$x^{2} + x - 3$
$3 x^{2} + 2 x$

x\left(3x+2\right)=
\left(x+3\right)\left(x-2\right)=
\left(6x^2-3x\right)\ :\ \left(3x\right)=
\frac{2x^3+4x}{2x}=

More like this

Võrrandid

Lineaarvõrrand ja võrre

Lineaarvõrrand

Lahendamine

ax+b=0

ax=-b| :\ a

x=-\frac{b}{a}

Näide

3x+6=0

3x=-6| :\ 3

x=\frac{-6}{3}=2

Võrdekujuline võrrand

\frac{a}{b}=\frac{c}{d}\ ⇒ ad=bc

Näide

\frac{2}{5}=\frac{6}{x}\ ⇒ 2\cdot x=5\cdot6\ 2x=30 ja x=15

Korda reeglit

–4
–3
3
4

-3x=12	x=
5x-20=0	x=
24+8x=0	x=
-4x-16=0	x=

–5
5
–10
10

\frac{x}{4}=\frac{15}{12}	x=
\frac{-6}{x}=\frac{3}{-5}	x=
\frac{10}{-40}=\frac{x}{20}	x=

Mittetäielik ruutvõrrand

ax² + c = 0

Kaks lahendit

-3x^2+12=0

–3x² = –12 |:(–3)

x^2=4

x_1=\sqrt{4}=2

x_2=-\sqrt{4}=-2

Lahendid puuduvad

3x^2+12=03x² = –12 |:3 x^2=-4Lahendid puuduvad,sest ühegi reaalarvu ruut pole negatiivne.

ax² + bx = 0

Alati on kaks lahendit, millest üks on null.x^2-6x=0x\left(x-6\right)=0Korrutis on null, kui vähemalt üks teguritest on null.

x_1=0

x-6=0

x_2=6

Korda reeglit

Leia võrrandi lahendid.

x^2-100=0

–10
0
10
lahend puudub

2x^2+50=0

–5
0
5
lahend puudub

10x+x^2=0

–10
0
10
lahend puudub

5x^2-25x=0

–5
0
5
lahend puudub

Täielik ruutvõrrand

ax² + bx + c = 0

x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}Juurealust avaldist nimetatakse diskriminandiks D.D=b^2-4ac

x² + px + q = 0

Täielik taandatud ruutvõrrand, sest a = 1.

x_{1,2}=-\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q}

Taandatud ruutvõrrandi x² + px + q = 0 lahendite korrutis on võrdne vabaliikmega ja lahendite summa on võrdne lineaarliikme kordaja vastandarvuga.x_1\cdot x_2=q

x_1+x_2=-p

Korda reeglit

Ruutvõrrandi 2x^2-11x+5=0diskriminant

D = ja lahendid

0
–0,5
0,5
–5
5
puuduvad

Ruutvõrrandi x^2+2x-15=0 lahendite summa on ja lahendite korrutis on

Lahendid

2
–15
3
–3
–5
5
–2
15
puuduvad

More like this

Võrdeline, lineaarne ja pöörvõrdeline seos

Võrdeline, lineaarne ja pöördvõreline seos

Võrdeline seos

a=\frac{y}{x}\ ⇒\ y=ax

Graafikuks on sirge, mis

on tõusev, kui a > 0;
on langev, kui a < 0.
läbib alati punkti\left(0;\ 0\right).

Lineaarfunktsioon

y=ax+b

Graafikuks on sirge, mis

lõikab x-telge, kui y=0;
lõikab y-telge, kui x=0;
läbib alati punkti\left(0;\ b\right).

Pöördvõrdeline seos

xy=a\ ⇒ y=\frac{a}{x},\ x\ne0

Graafikuks on hüperbool, mis asub

I ja III veerandis, kui a > 0;
II ja IV veerandis, kui a < 0.

Korda reeglit

$y = 3 x$
$x y = 9$
$y = \frac{2}{x}$
$y = \frac{1}{2} x$
$y = \frac{-3}{x}$
$y = - 9 x + 1$

(0; 0)
(0; 2)
(0; –2)
(0; 3)
(0; –3)
(2; 0)
(–2; 0)
(–3; 0)
(3; 0)

Sirge	Lõikepunkt x-teljega	Lõikepunkt y-teljega
y=3x
y=x+3
y=2-x

Punkt (4; 1) y=\frac{4}{x} graafikul.
Punkt (–2; 5) y=-\frac{10}{x} graafikul.
Punkt (–2; –4) y=-\frac{8}{x} graafikul.
Punkt (5; 0) y=\frac{5}{x} graafikul.
Punkt (3; –5) y=-\frac{15}{x} graafikul.

More like this

Ruutfunktsioon

y=ax^2+bx+c

Graafik on parabool.
Parabool avaneb üles, kui a > 0.
Parabool avaneb alla, kui a < 0.
Nullkohad on vastava ruutvõrrandi lahendid x_1 ja x_2.
Haripunkti abstsiss x_h=-\frac{b}{2a}\ või x_h=\frac{x_1+x_2}{2}.

y = ax²

Graafik läbib alati punkti \left(0;\ 0\right).
Nullkohad x_1=x_2.
Vastava ruutvõrrandi diskriminant on D=b^2-4ac=0.

y = ax² + c

Graafik läbib alati punkti \left(0;\ c\right),mis on ühtlasi haripunkt.
Kui D > 0, siis on kaks nullkohta.
Kui D < 0, siis nullkohad puuduvad.

y = ax² + bx

Graafik läbib alati punkti (0; 0).
Kaks nullkohta:
x_1=0 ja x_2.
D=b^2-4ac>0

y = ax² + bx + c

Graafik läbib alati punkti \left(0;\ c\right).
Kui D > 0, siis on kaks nullkohta.
Kui D < 0, siis nullkohad puuduvad.
Kui D = 0, siis on üks nullkoht.

Korda reeglit

Uuri funktsiooni.

y=x^2-9

Funktsiooni graafikuks on mis avaneb
Nullkohad:
Haripunkt H

y=-x^2-9

Funktsiooni graafikuks on mis avaneb
Nullkohad:
Haripunkt H

y=-x^2+3x

Funktsiooni graafikuks on mis avaneb
Nullkohad:
Haripunkti abstsiss x_h =

y=x^2-2x-3

Funktsiooni graafikuks on mis avaneb
Nullkohad:
Graafik lõikab y-telge punktis
Haripunkt H

More like this

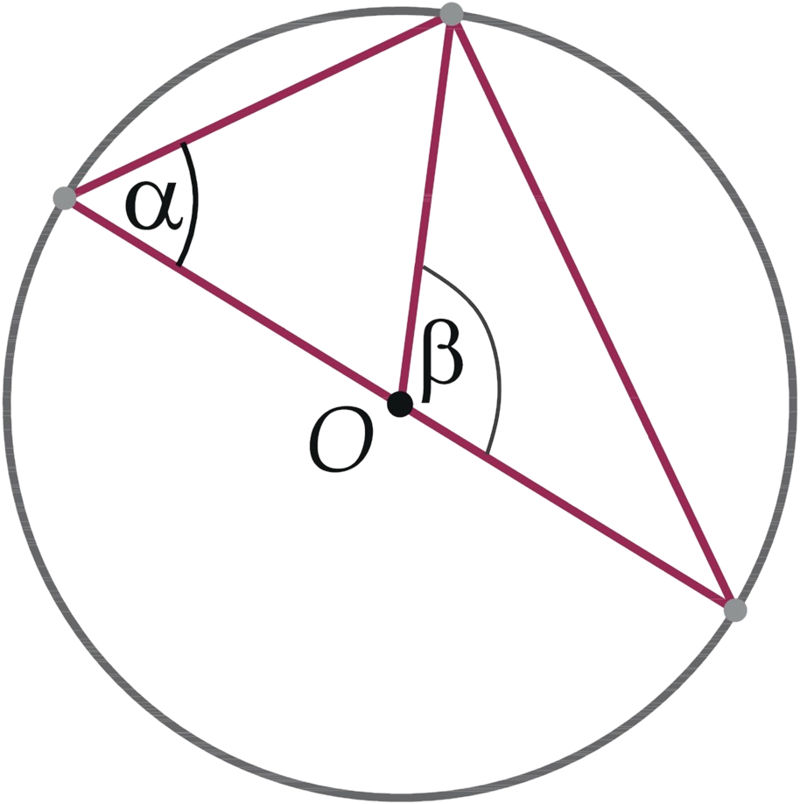
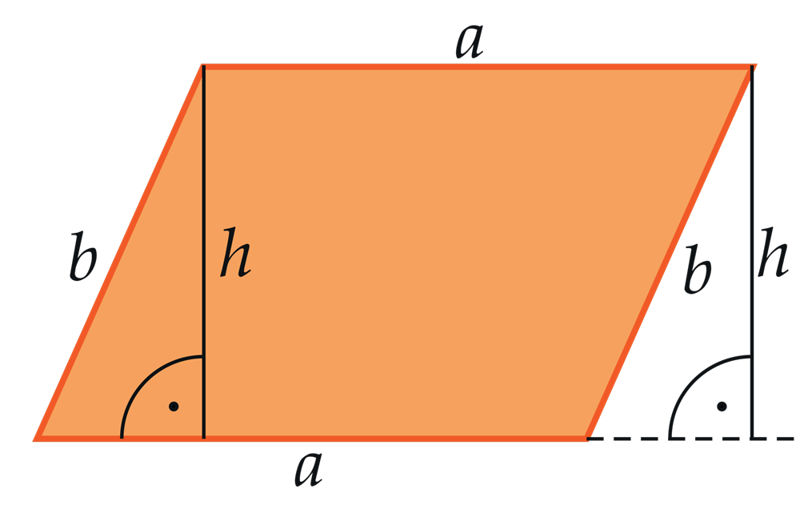
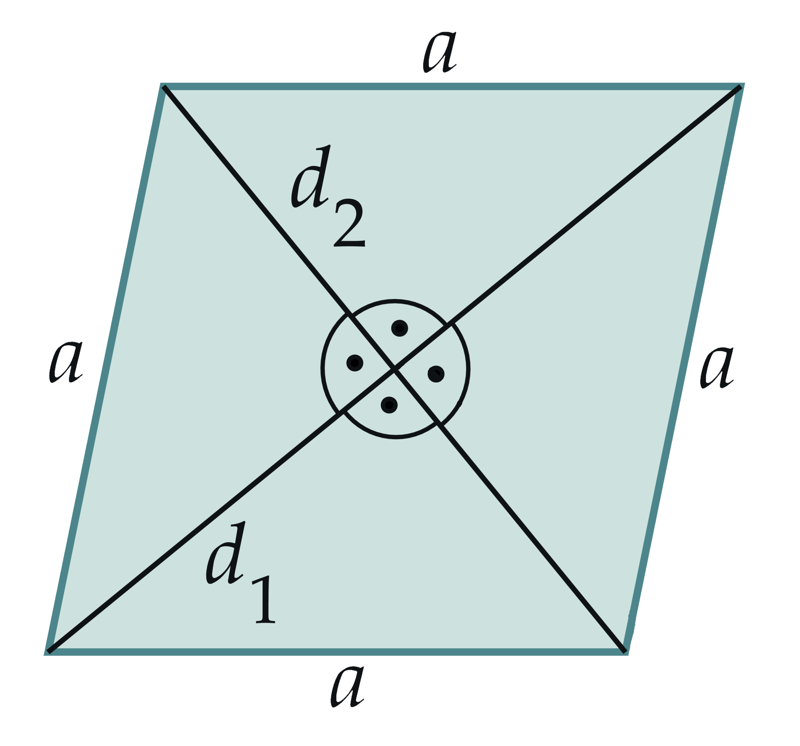
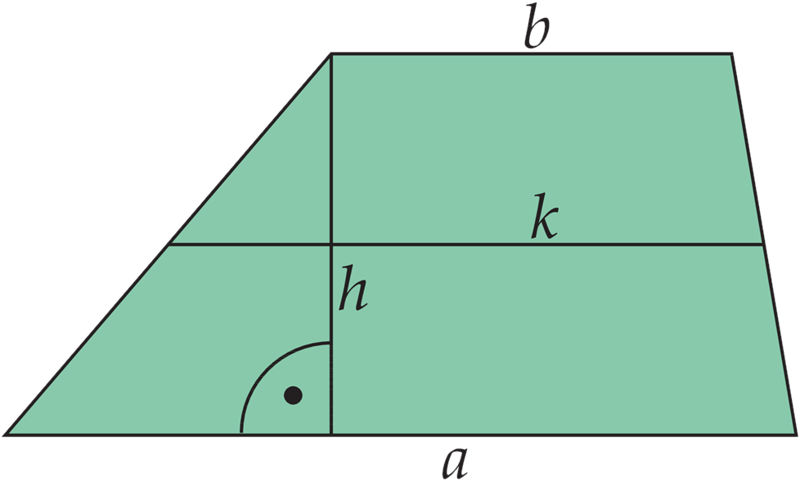
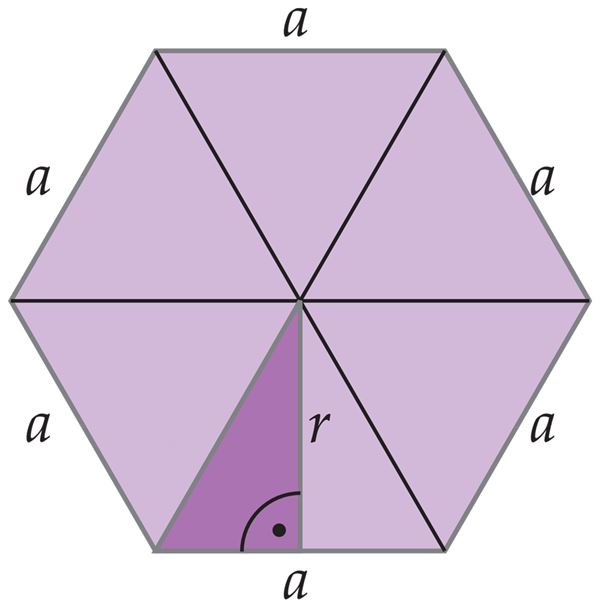
Geomeetria

Nurgad hulknurgas ja paralleelide vahel

Nurgad hulknurgas

n-nurga nurkade summa

S_n=\left(n-2\right)\cdot180\degree.

Näide

Leiame seitsenurga nurkade summa.

S_7=\left(7-2\right)\cdot180\degree=900\degree

Seitsenurk

Korrapärane n-nurk

Ühe sisenurga suurus

\mathrm{\alpha}=\frac{\left(n-2\right)\cdot180\degree}{n}

või

\mathrm{\alpha=}180\degree-\frac{360\degree}{n}.

Näide

Korrapärase viisnurga nurk

\mathrm{\alpha=}180\degree-\frac{360\degree}{5}=108\degree.

Korrapärane viisnurk

Joonisel on paralleelsed sirged s ja t.

s\parallel t

Sellisel juhul

tekivad võrdsed põiknurgad

\angle4=\mathrm{\beta,\ }\angle3=\mathrm{\alpha},

lähisnurkade summa on 180°.

\angle4+\mathrm{\alpha}=180\degree

\angle3+\mathrm{\beta}=180\degree

180°
360°
3
4
5

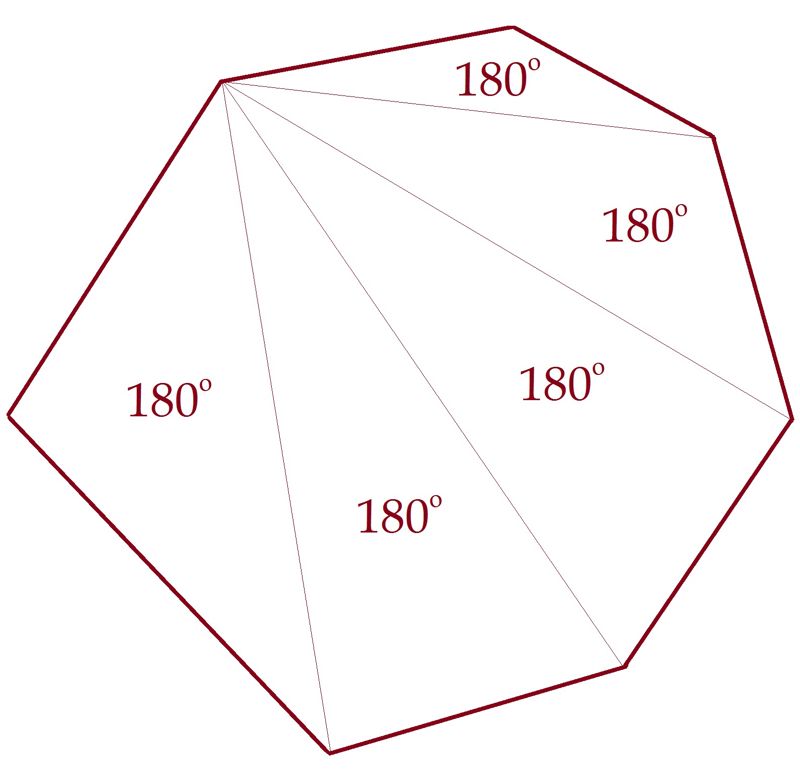
kolmnurk

ruut

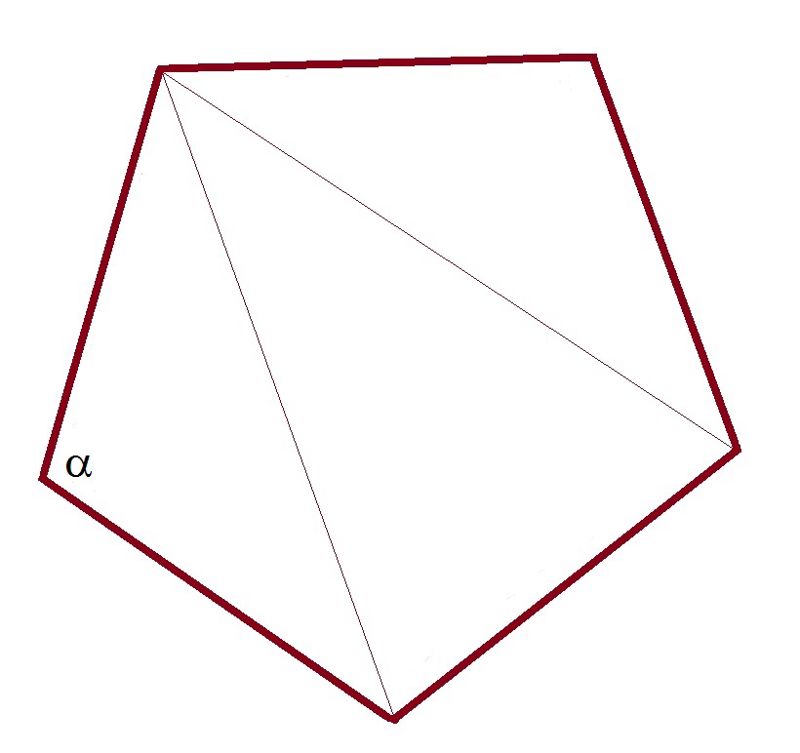
viisnurk ⋅ 180°

kuusnurk ⋅ 180°

seitsenurk ⋅ 180°

Ring

Pindala, ümbermõõt, puutuja

Diameeter on kaks korda pikem kui raadius.
Puutuja on risti puutepunkti tõmmatud raadiusega (vt joonist).
Ümbermõõt
C=2\cdot\pi\cdot r
Pindala
S=\pi\cdot r^2

Nurgad ringis

Täisring on 360°.
Kesknurk on kaks korda suurem samale kaarele toetuvast piirdenurgast.
Samale kaarele toetuvad piirdenurgad on võrdsed.

Thalese teoreem

Diameetrile toetuv piirdenurk on täisnurk.

Kui α = 70°, siis β =
Kui β = 70°, siis α =
Kolmnurk, mille üks külg on diameeter, on

Hulknurk

Rööpkülik

Vastasküljed on paralleelsed.
Vastasküljed on võrdsed.
Ümbermõõt
P=2a+2b.
Pindala
S=a\cdot h.

Romb

Küljed on võrdsed.
Diagonaalid on risti.
Ümbermõõt
P=4\cdot a.
Pindala
S=\frac{d_1\cdot d_2}{2}.

Trapets

Alused a ja b on paralleelsed.
Kesklõik k on aluste poolsumma.
S=\frac{a+b}{2}\cdot h
S=k\cdot h

Korrapärane hulknurk

Korrapärane kuusnurk

Jaotub võrdhaarseteks kolmnurkadeks.

r – apoteem
n - külgede arv
S=n\cdot\frac{a\cdot r}{2}
P=n\cdot a

Ainult korrapärane kuusnurk jaotub võrdkülgseteks kolmnurkadeks.

Korda reeglit

Leia pindala ja ümbermõõt.

a = 12 cm, b = 10 cm, h_a = 8 cm

30
44
80
96
120

S = cm²

P = cm

d₁ = 24 cm, d₂ = 10 cm, a = 13 cm

40
47
52
96
120
130
240

S = cm²

P = cm

a = 15 cm, b = 10 cm, h = 12 cm,
haarad 12 cm ja 13 cm

50
62
120
150

S = cm²

P = cm

a = 10 cm, r ≈ 12 cm

80
96
240
480
960

S ≈ cm²

P = cm

Kolmnurk

Nurkade summa on 180°.
Pindala S=\frac{ah}{2}.

Kesklõik

Ühendab kolmnurga kahe külje keskpunkte.
On paralleelne küljega.
On kaks korda lühem kui sellega paralleelne külg.

Näide

EF\parallel BC

BC=2\cdot EF

Mediaan

Ühendab kolmnurga tippu vastaskülje keskpunktiga.
Mediaanide lõikepunkt jaotab mediaani suhtes 2 : 1 tipust alates.

Näide

AO=2\cdot OD

5
6
7
10
12
14

Täisnurkne kolmnurk

Pythagorase teoreem

Trigonomeetrilised funktsioonid

siinus\mathrm{ }=\frac{\mathrm{vastaskaatet}}{\mathrm{hüpotenuus}}
\sin\alpha=\frac{a}{c}
koosinus=\frac{\mathrm{lähiskaatet}}{\mathrm{hüpotenuus}}
\cos\alpha=\frac{b}{c}
tangens\mathrm{=\frac{\mathrm{vastaskaatet}}{lähiskaatet}}
\tan\alpha=\frac{a}{b}

5
8
12
15
17
25

a	b	c
3	4
12		13
	6	10
8	15

Sarnased kujundid

Vastavate külgede suhe on konstantne.
Vastavad nurgad on võrdsed.
Üks kujund on teise suurendatud või vähendatud kujutis.
Külgede ja ümbermõõtude suhe on sarnasustegur k.
Pindalade suhe on k².

NN

Kolmnurkade sarnasuse tunnus nurk-nurk

Kui ühe kolmnurga kaks nurka on vastavalt võrdsed teise kolmnurga kahe nurgaga, siis on need kolmnurgad sarnased.

Kolmnurgad on sarnased. Mõlema kolmnurga kolmas nurk on 39°

KKK

Kolmnurkade sarnasuse tunnus külg-külg-külg

Kui ühe kolmnurga küljed on vastavalt võrdelised teise kolmnurga külgedega, siis on need kolmnurgad sarnased.

Kolmnurgad on sarnased. \frac{16}{8}=\frac{14}{7}=\frac{19}{9,5},\ k=2

KNK

Kolmnurkade sarnasuse tunnus külg-nurk-külg

Kui ühe kolmnurga kaks külge on võrdelised teise kolmnurga kahe küljega ja nende külgede vahelised nurgad on võrdsed, siis on need kolmnurgad sarnased.

\frac{5}{10}=\frac{6}{12},\ k=0,5\ ja nurk 100°

Korda reeglit

ruudud on sarnased.
ringid on sarnased.
rombid on sarnased.
täisnurksed kolmnurgad on sarnased.
võrdkülgsed kolmnurgad on sarnased.

Ühe täisnurkse kolmnurga üks teravnurk on 55°.

Teise täisnurkse kolmnurga üks teravnurk on 35°.

Need kolmnurgad sarnased.

Ühe kolmnurga küljed on 5 cm, 6 cm ja 8 cm.

Teise kolmnurga küljed on 10 cm, 12 cm ja 16 cm.

Need kolmnurgad sarnased.

Ühe kolmnurga nurk on 53° ning selle nurga lähisküljed on 10 cm ja 14 cm.

Teise kolmnurga üks nurk on 53° ning selle nurga lähisküljed on 10 cm ja 7 cm.

Need kolmnurgad sarnased.

More like this

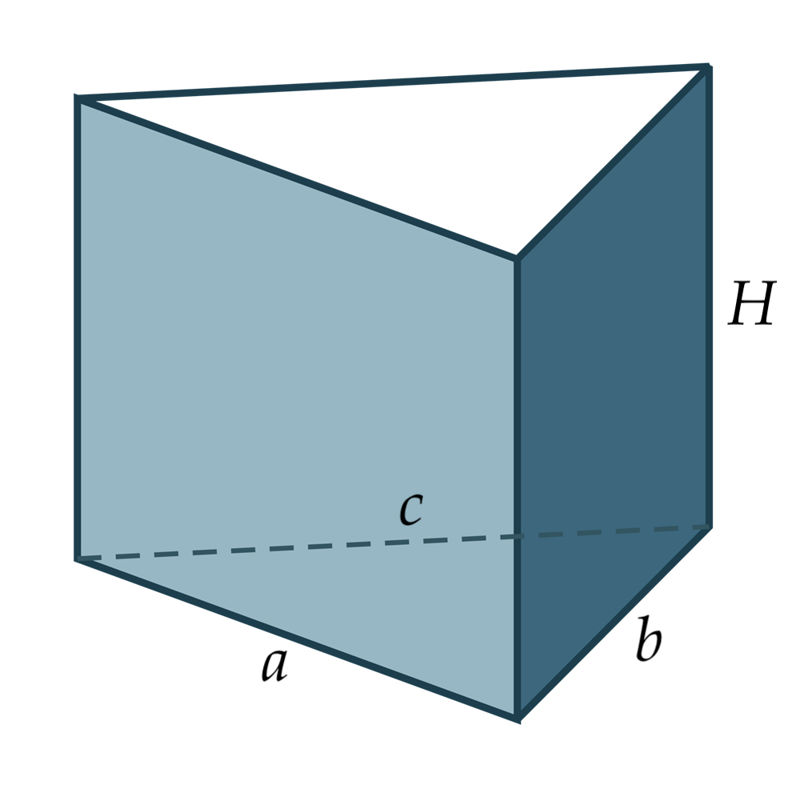
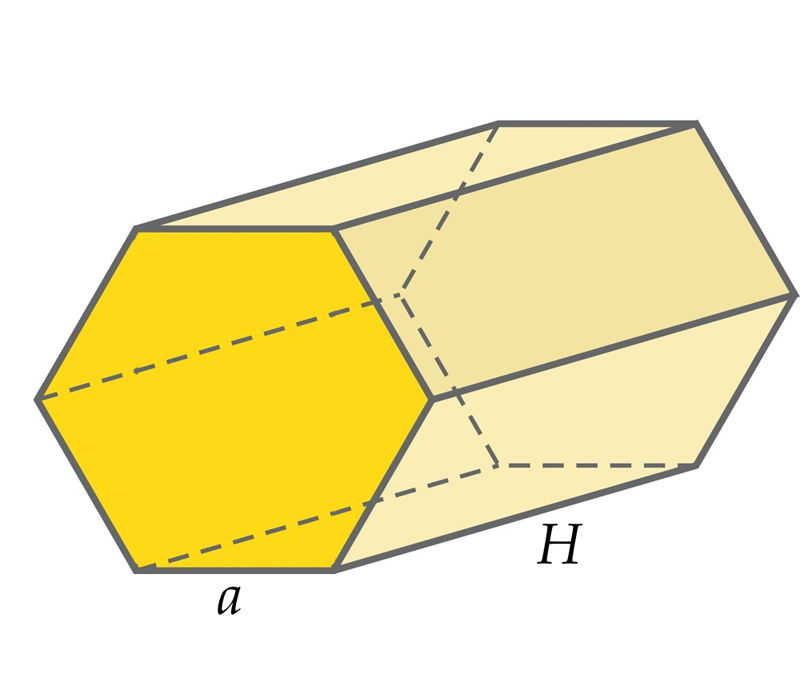
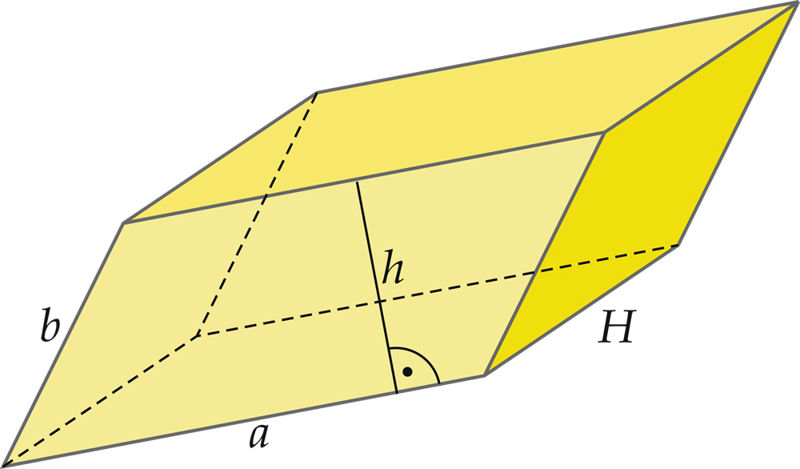
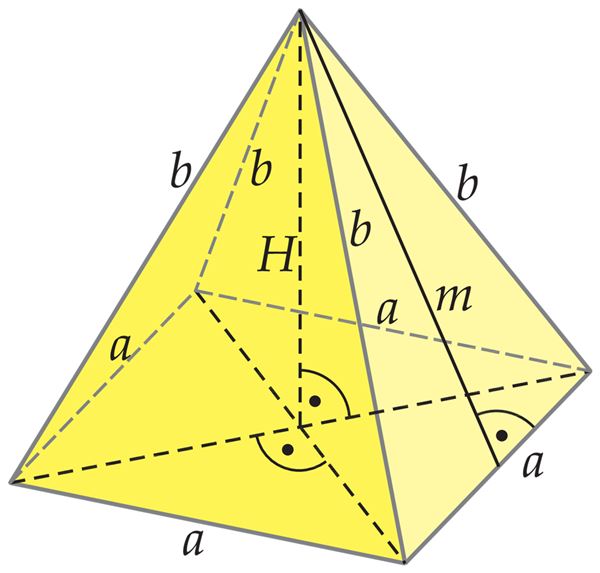
Stereomeetria

Püstprisma

Kolmnurkse püstprisma põhi on kolmnurk

Prisma kaks paralleelset põhja on võrdsed hulknurgad.
Põhja ümbermõõt P on kõikide põhiservade summa.
Põhja pindala S_p on vastava hulknurga pindala.
Täispindala S_t on kõikide tahkude pindalade summa.
Ruumala V on põhja pindala S_p ja kõrguse H korrutis.

Kuusnurkse prisma põhi on kuusnurk

Külgpindala

S_k=PH

Täispindala

S_t=2\cdot S_p+S_k

Ruumala

V=S_p\cdot H

Püströöptahuka põhi on rööpkülik külgedega a ja b

Põhja pindala

Põhjadeks on rööpkülikud.

S_p=a\cdot h

Külgpindala

S_k=P\cdot H

P=2a+2b

Prisma pinnad

Püramiid

Korrapärane nelinurkne püramiid

Põhjaks ruut

S_p=a^2

Külgpindala

S_k=4\cdot\frac{am}{2}

Ruumala

V=\frac{S_p\cdot H}{3}

Korrapärane püramiid

Põhi on korrapärane hulknurk ümbermõõduga P ja pindalaga S_p.
Külgtahud on võrdsed võrdhaarsed kolmnurgad.
Kõrgus H on tipu kaugus põhjast.
Külgpindala S_k on kõikide külgtahkude pindalade summa.
Täispindala S_t on kõikide tahkude pindalade summa.

Korrapärased (1, 2, 3, 7, 8) ja mittekorrapärased (4, 5, 6) püramiidid

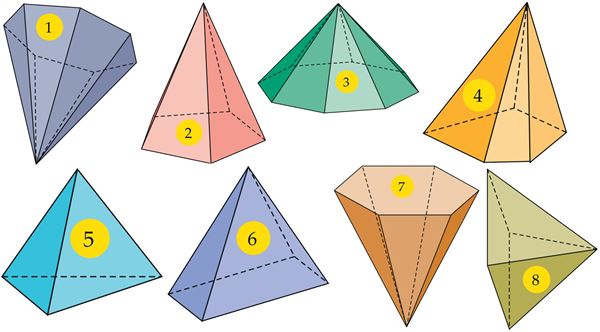
Püramiidi pinnad

Silinder

Kõrgus H

Raadius r

Külgpindala

Külgpind on ristkülik.

S_k=C\cdot H=2\pi r\cdot H

Põhja pindala

Põhi on ring.

S_p=\pi r^2

Täispindala

Kõikide pindade summa.

S_t=2\cdot S_p+S_k

Ruumala

Põhja pindala ja kõrguse korrutis.

V=S_p\cdot H

V=\pi r^2\cdot H

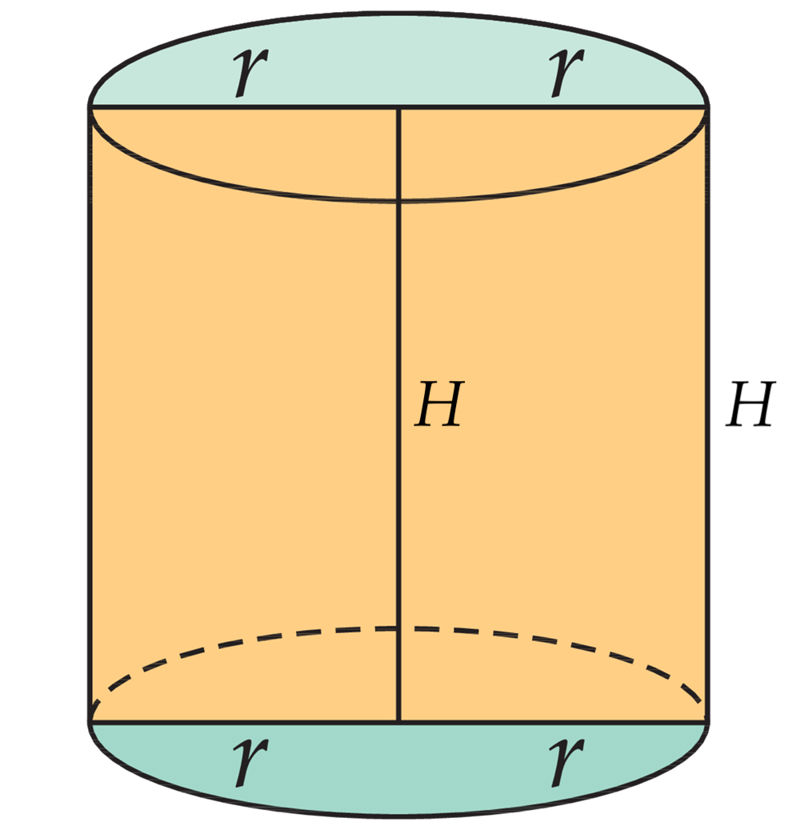
Silindri pinnad

Koonus

Kõrgus H

Moodustaja m

Raadius r

Külgpindala

Külgpind on sektor.

S_k=\pi rm

Põhja pindala

Põhi on ring.

S_p=\pi r^2

Täispindala

Kõikide pindade summa.

S_t=S_p+S_k

Ruumala

Kolmandik põhja pindala ja kõrguse korrutisest.

V=\frac{S_p\cdot H}{3}

V=\frac{\pi r^2\cdot H}{3}

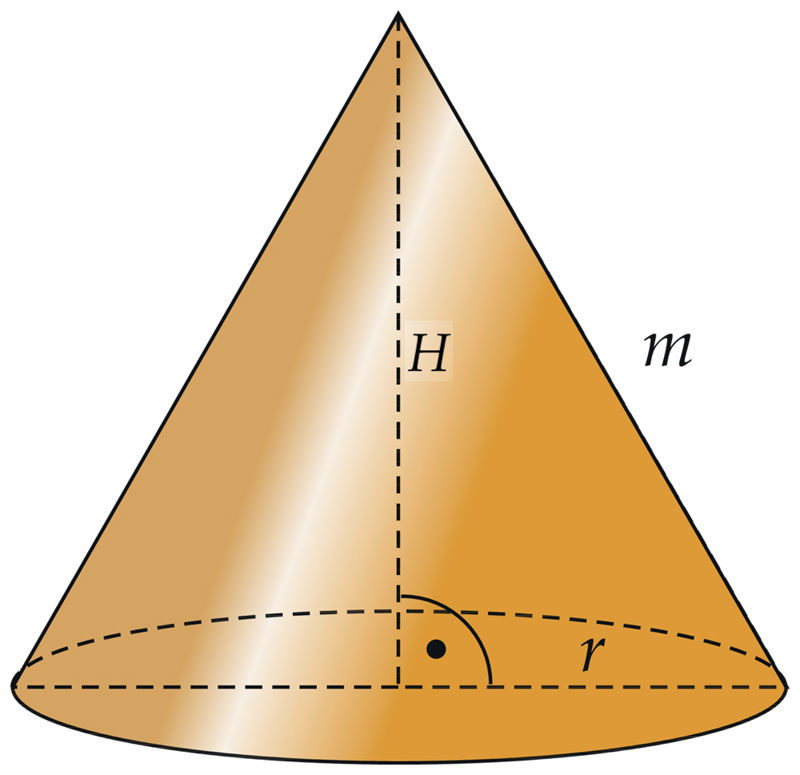
Koonuse pinnad

Kera

Kera raadius r

Ruumala

V=\frac{4}{3}\pi r^3

Pindala

S=4\pi r^2

Idee, kuidas jaotada kera pinda.

More like this

Service provided by Star Cloud LLC

Join Opiq

Opiq score

	Tasks
	Chapter is studied

Valemid ja reeglid

More like this

Aritmeetika

Tehted ratsionaalarvudega

Liitmine ja lahutamine

Reegel

Näide

Korrutamine

Reegel

Näide

Jagamine

Reegel

Näide

Nulli jagatises

Reegel

Näide

Korda reeglit

Vastandarv ja absoluutväärtus

Vastandarv

Reegel

Näide

Absoluutväärtus

Reegel

Näide

Järjestamine

Reegel

Näide

Korda reeglit

Märka sümboleid

More like this

Kiirus, aeg, teepikkus

Ühtlane liikumine

Teepikkus

Kiirus

Aeg

Teisendamine

More like this

Protsent

Protsent

Mis on protsent?

Mis on osa ja osamäär?

Mis on promill?

Sõber soovitab

Märka protsenti

Korda reeglit

More like this

Algebra

Tehted astemetega

Abivalemid

Korda reeglit

More like this

Võrrandid

Lineaarvõrrand ja võrre

Lineaarvõrrand

Lahendamine

Näide

Võrdekujuline võrrand

Näide

Korda reeglit

Mittetäielik ruutvõrrand

ax2 + c = 0

Kaks lahendit

Lahendid puuduvad

ax2 + bx = 0

Korda reeglit

Täielik ruutvõrrand

ax2 + bx + c = 0

x2 + px + q = 0

Korda reeglit

More like this

Võrdeline, lineaarne ja pöörvõrdeline seos

Võrdeline, lineaarne ja pöördvõreline seos

Võrdeline seos

Lineaarfunktsioon

Pöördvõrdeline seos

Korda reeglit

More like this

Ruutfunktsioon

Ruutfunktsioon

y = ax2

ax² + c = 0

ax² + bx = 0

ax² + bx + c = 0

x² + px + q = 0

y = ax²

y = ax² + c

y = ax² + bx

y = ax² + bx + c