Peatükk 1.1 (Математика 10)

Натуральные, целые и рациональные числа

Понятие числа начало формироваться тысячи лет назад, совершенствуясь и обогащаясь вместе с развитием человеческой цивилизации. Уже в древнем обществе возникла необходимость сравнивать множества, что стало возможным посредством счета элементов этих множеств. Так возникло первое из изученных нами в школьном курсе числовых множеств – множество N натуральных чисел:

N = {0; 1; 2; 3; ...}.

Поскольку число 0 не столь естественным образом возникает при счете предметов, то неудивительно, что это число было введено в употребление значительно позднее. Только в VII веке индийскими математиками были сформулированы правила пользования числом 0.

Нами изучены четыре основных действия с натуральными числами. Это сложение и умножение, а также обратные к ним действия – вычитание и деление.

Задание 1. Натуральные числа

№

a

b

a + b

a · b

a – b

a : b

1.

3

7

10

21

–4

\frac{3}{7}

2.

3.

4.

5.

6.

Из предыдущего задания мы видим, что разность 3 – 7 не является натуральным числом. Таким образом, зная только натуральные числа, нельзя выполнить вычитание во всех случаях. Отсюда вытекает необходимость дополнения множества натуральных чисел такими числами, которые позволяли бы всегда выполнять вычитание в полученном более широком множестве чисел. Это становится возможным, если ввести в употребление числа, противоположные натуральным.

Для натурального числа n противоположное число –n мы определяем таким образом, что

n + (–n) = 0.

Натуральные числа вместе с противоположными им числами образуют множество Z целых чисел:

Z = {...; – 2; –1; 0; 1; 2; ...}.

Отдельно рассматривают также множество Z+ положительных целых чисел:

Z+ = {1; 2; 3; ...}

и множество Z– отрицательных целых чисел:

Z– = {...; –3; –2; –1}.

Таким образом,

Z = Z– ∪ {0} ∪ Z+   и   N ⊂ Z  (рис. 1.1).

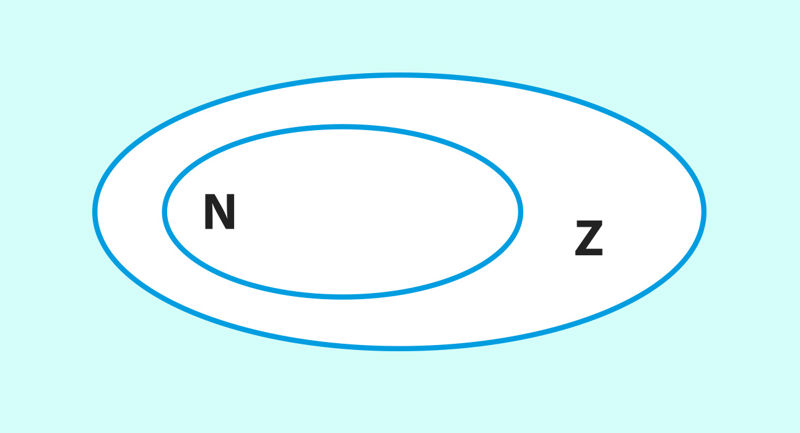Рис. 1.1

В результате введения противоположных чисел действие вычитания можно рассматривать как сложение (а разность – как сумму):

a – b = a + (–b).

Так как для всякого целого числа существует противоположное ему число, то действие вычитания на множестве целых чисел всегда выполнимо – разность любых двух целых чисел всегда является целым числом.

Целые числа подразделяются еще на четные и нечетные. Целое число, делящееся на 2, называется четным числом. Taкое число представляется в виде 2n, где n ∈ Z. Нечетные, т. е. не делящиеся на 2, числа можно преставить в виде 2n + 1, гдe n ∈ Z.

Задание 2. Целые числа

№

a

b

a + b

a · b

a – b

a : b

1.

3

7

10

21

–4

\frac{3}{7}

2.

3.

4.

5.

6.

Из только что решенного задания вытекает, что частное от деления целых чисел не обязательно целое число. Если число a делится на число b (b ≠ 0), то частное является целым числом, в противном же случае оно оказывается дробным числом ab. Если a и b – числа одного знака, то эта дробь положительна, если разного знака, то отрицательна.

Дополнив множество целых чисел дробными числами, мы получим новое числовое множество, в котором всегда выполнимо и действие деления (кроме деления на нуль). Все целые числа, а также все положительные и отрицательные дробные числа вместе образуют множество Q рациональных чисел (рис. 1.2).

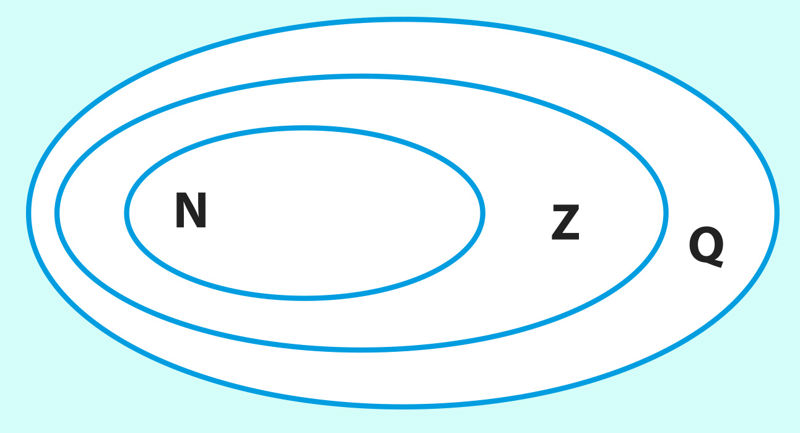
Рис. 1.2

Поскольку всякое целое число можно представить в виде частного \frac{a}{b} (например, -5=-\frac{10}{2}; 0=\frac{0}{2}), то мы можем дать теперь следующее определение:

рациональным числом называется всякое число, которое можно представить в виде дроби ab, где a ∈ Z, b ∈ Z и b ≠ 0.

При изучении дробей мы уже пользовались следующими понятиями:

обыкновенная дробь: ab (a ∈ N, b ∈ N и b ≠ 0),

правильная дробь: ab (a ∈ N, b ∈ N, b ≠ 0 и a < b),

неправильная дробь: ab (a ∈ N, b ∈ N, b ≠ 0 и a ≥ b),

смешанное число: сумма натурального числа и правильной дроби: 2\frac{1}{2}=2+\frac{1}{2},

десятичная дробь: дробь, которая записывается при помощи запятой, где первая цифра после запятой означает число десятых, вторая цифра – число сотых и т. д.: 3,75=3+\frac{7}{10}+\frac{5}{100}.

Одно и то же число может быть представлено несколькими различными способами: 1\frac{1}{2}=\frac{3}{2}=1,5.

Всякое рациональное число можно представить в виде десятичной дроби, разделив числитель на знаменатель. При этом результатом деления может быть:

  1. в первом случае конечная десятичная дробь:

\frac{51}{40}=1,275;

  1. во втором случае получающиеся при делении остатки начинают с некоторого момента повторяться, и возникает бесконечная периодическая десятичная дробь:

\frac{17}{6}=17\ :\ 6=2,833...=2,8\left(3\right).

Поскольку всякая конечная десятичная дробь может быть записана в виде бесконечной периодической десятичной дроби (1,275 = 1,27500… = 1,275(0)), то можно сказать, что:

всякое рациональное число представимо в виде бесконечной периодической десятичной дроби.

Имеет место и обратное утверждение:

всякая бесконечная периодическая десятичная дробь является записью рационального числа.

Пример.

Выразим бесконечную периодическую десятичную дробь x = 1,2(43) в виде обыкновенной дроби, т. е. в виде частного от деления двух целых чисел.

Решение.

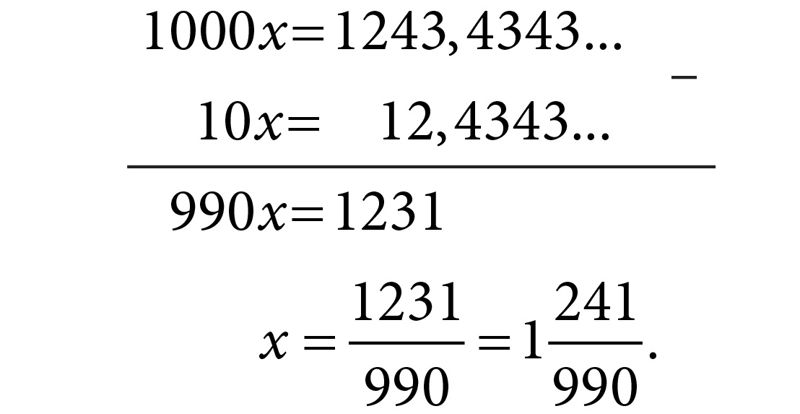a и 1a являются взаимно обратными числами.

Seotud sisu
Muud tegevused

Упражнения A

Задание 3. Натуральные, целые и рациональные числа
  • –1,5
  • 1212
  • 40
  • -75
  • 21,01
  • 10005
  • 12,5
  • –15
  • -23
  • 47
  • 15
  • 0
  • –40
  • 2,3
  • 0,005
  • –1,5
  • 1212
  • 40
  • -75
  • 21,01
  • 10005
  • 12,5
  • –15
  • -23
  • 47
  • 15
  • 0
  • –40
  • 2,3
  • 0,005
  • –1,5
  • 1212
  • 40
  • -75
  • 21,01
  • 10005
  • 12,5
  • –15
  • -23
  • 47
  • 15
  • 0
  • –40
  • 2,3
  • 0,005
  • –1,5
  • 1212
  • 40
  • -75
  • 21,01
  • 10005
  • 12,5
  • –15
  • -23
  • 47
  • 15
  • 0
  • –40
  • 2,3
  • 0,005
  • –1,5
  • 1212
  • 40
  • -75
  • 21,01
  • 10005
  • 12,5
  • –15
  • -23
  • 47
  • 15
  • 0
  • –40
  • 2,3
  • 0,005
  • –1,5
  • 1212
  • 40
  • -75
  • 21,01
  • 10005
  • 12,5
  • –15
  • -23
  • 47
  • 15
  • 0
  • –40
  • 2,3
  • 0,005
  • –1,5
  • 1212
  • 40
  • -75
  • 21,01
  • 10005
  • 12,5
  • –15
  • -23
  • 47
  • 15
  • 0
  • –40
  • 2,3
  • 0,005
  • –1,5
  • 1212
  • 40
  • -75
  • 21,01
  • 10005
  • 12,5
  • –15
  • -23
  • 47
  • 15
  • 0
  • –40
  • 2,3
  • 0,005
  • –1,5
  • 1212
  • 40
  • -75
  • 21,01
  • 10005
  • 12,5
  • –15
  • -23
  • 47
  • 15
  • 0
  • –40
  • 2,3
  • 0,005
  • –1,5
  • 1212
  • 40
  • -75
  • 21,01
  • 10005
  • 12,5
  • –15
  • -23
  • 47
  • 15
  • 0
  • –40
  • 2,3
  • 0,005
Задание 4. Дроби
  • –1,5
  • 1212
  • 40
  • -75
  • 21,01
  • 10005
  • 12,5
  • –15
  • -23
  • 47
  • 15
  • 0
  • –40
  • 2,3
  • 0,005
  • –1,5
  • 1212
  • 40
  • -75
  • 21,01
  • 10005
  • 12,5
  • –15
  • -23
  • 47
  • 15
  • 0
  • –40
  • 2,3
  • 0,005
  • –1,5
  • 1212
  • 40
  • -75
  • 21,01
  • 10005
  • 12,5
  • –15
  • -23
  • 47
  • 15
  • 0
  • –40
  • 2,3
  • 0,005
  • –1,5
  • 1212
  • 40
  • -75
  • 21,01
  • 10005
  • 12,5
  • –15
  • -23
  • 47
  • 15
  • 0
  • –40
  • 2,3
  • 0,005
Задание 5. Натуральные, целые и рациональные числа
  1. натуральными числами;
  2. ни целыми числами, ни обыкновенными дробями;
  3. целыми числами;
  4. ни натуральными числами, ни десятичными дробями.
Задание 6. Натуральные, целые и рациональные числа
  1. не являются целыми числами;
  2. не являются целыми положительными числами;
  3. являются рациональными числами;
  4. являются целыми числами.
Задание 7. Натуральные, целые и рациональные числа
  • Всякое натуральное число является целым числом.
  • Всякое рациональное число является целым числом.
  • Ни одно целое число не является рациональным числом.
  • Любое натуральное число положительно.
  • Существуют рациональные числа, не являющиеся целыми числами.
  • Существуют натуральные числа, не являющиеся рациональными числами.
  • Существуют целые числа, являющиеся натуральными числами.
  • Существует натуральное число, не являющееся положительным.
  • Всякая обыкновенная дробь является целым числом.
  • Всякое натуральное число можно представить в виде обыкновенной дроби.
  • Существуют обыкновенные дроби, являющиеся целыми числами.
  • Существует правильная дробь, являющаяся натуральным числом.
Задание 8. Противоположные и обратные числа

Ответ:  число, противоположное сумме чисел 7 и –13, есть  .

Ответ: для чисел 7 и –13 разность противоположных им чисел есть .

Ответ: для чисел 7 и –13 число, обратное их разности, равно .

Ответ: для чисел 7 и –13 сумма обратных им чисел есть .

Ответ: для чисел 7 и –13 частное от деления разности обратных им чисел на сумму противоположных им чисел есть .

Ответ: для чисел 7 и –13 произведение суммы противоположных им чисел на разность обратных им чисел есть .

Задание 9. Перевод обыкновенной дроби в десятичную

716 = 

8180 = 

-925 = 

79 = 

23 = 

-518 = 

Задание 10. Представление десятичной дроби в виде частного от деления двух целых чисел

0,(5) = 

1,34(5) = 

0,4(12) = 

0,(9) = 

1,(4) = 

0,7(5) = 

2,2(34) = 

3,(9) = 

Seotud sisu
Muud tegevused

Упражнения Б

Задание 11. Конечная или бесконечная десятичная дробь?

\frac{7}{16}

\frac{81}{80}

-\frac{9}{25}

\frac{7}{9}

\frac{2}{3}

-\frac{5}{18}

  1. У каких дробей знаменатели имеют своими простыми делителями лишь степени чисел 2 и 5?
  2. Какие несократимые дроби выражаются конечными десятичными дробями, а какие нет?
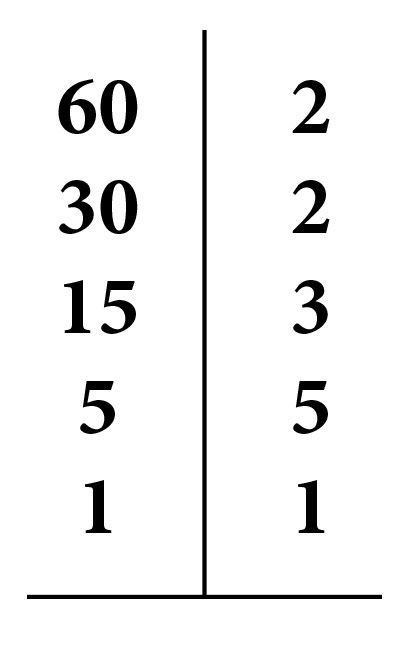
  1. Обоснуйте высказанную в пункте 2 гипотезу. Для этого изучите следующий пример:
    \frac{3}{40}=\frac{3}{2\cdot2\cdot2\cdot5}=\frac{3\cdot5\cdot5}{2\cdot5\cdot2\cdot5\cdot2\cdot5}=\frac{75}{1000}=0,075
Задание 12. Представление десятичной дроби в виде частного от деления двух целых чисел

0,(7) = ,

0,(76) =  и

0,(765) = .

Сформулируйте правило преобразования в обыкновенную дробь аналогичных бесконечных периодических десятичных дробей.

Задание 13. Представление десятичной дроби в виде частного от деления двух целых чисел

0,2(5) = ;

0,2(54) = ;

0,2(543) =  и

0,12(54) = .

Сформулируйте правило преобразования в обыкновенную дробь аналогичных десятичных дробей.

Seotud sisu
Muud tegevused
Palun oota