Tunni ülesehitus
- Millega tegeleme 3. perioodil? 5 min
- Geomeetrilised kujundid, 30 min
- Hulknurgad, 25 min
- Ümbermõõdu, pindala ja ruumala arvutamine, 15 min
- Kokkuvõte, 15 min
Ettevalmistus
Õpetaja prindib välja bingokaardid ja soovi korral töölehed.
Eelteadmised
Õpilane
- nimetab tasandilisi ja ruumilisi kujundeid;
- arvutab ristküliku, ruudu ja kolmnurga ümbermõõtu;
- arvutab ristküliku ja ruudu pindala;
- arvutab risttahuka ja kuubi pindala ning ruumala.
Tunni eesmärgid
Õpilane tuletab meelde
- õpitud tasandilised ja ruumilised kujundid;
- õpitud tasandiliste kujundite ümbermõõdu ja pindala arvutamiseks vajalikud valemid;
- risttahuka ja kuubi pindala ning ruumala valemid.
Seotud materjal
- ptk 6.1 „Kordamine. Geomeetrilised kujundid“
Märksõnad ja meetodid
- Tasandilised ja ruumilised kujundid, pindala, ümbermõõt, ruumala
- Ajurünnak, arutelu, iseseisev töö, liikumisharjutus (tõene/väär), oskuste bingo, animatsioonid
Lõiming
- Matemaatika 1. kl (ristkülik ja risttahukas, ruut ja kuup, ring ja kera, kolmnurk ja püramiid)
- Matemaatika 2. kl (kolmnurk, risttahukas ja kuup)
- Matemaatika 3. kl (hulknurgad, ristkülik ja ruut, ristküliku ja ruudu ümbermõõt, ringjoon ja ring, kolmnurk, ruumilised kujundid)
- Matemaatika 4. kl (ristküliku ja ruudu pindala, kolmnurk, kolmnurga ümbermõõt)
- Matemaatika 5. kl (punkt ja sirglõik, murdjoon, kiir, sirge, tasand, nurk, hulknurgad, risttahuka ja kuubi pindala, risttahuka ja kuubi ruumala)
Läbivad teemad
- Kultuuriline identiteet (geomeetria vajalikkus)
- Tervis ja ohutus (liikumine ainetunnis)
- Tehnoloogia ja innovatsioon (Opiqu kasutamine)
Millega tegeleme 3. perioodil?
5
- Millega tegeleme 3. perioodil?
- Milliseid vahendeid on tundides vaja?
1. ja 2. perioodil õppisid õpilased arvutama harilike murdudega ja lahendama protsentülesandeid. 3. perioodi teemad on seotud geomeetriaga. Õpetaja selgitab, milliseid vahendeid läheb õpilastel tundides vaja (joonlaud, korralikult teritatud harilik pliiats, kustutuskumm, sirkel, värvilised pliiatsid, mall, taskuarvuti).
Geomeetrilised kujundid
30
- Mis on geomeetria?
- Ajurünnak: milliseid geomeetrilisi kujundeid sa tead? Opiq ptk 6.1 ül 1
- Arutelu: kuidas on kujundid omavahel seotud?
- Opiq ptk 6.1 ül 2, 3
- Ümbermõõdu, pindala ja ruumala valemid, Opiq ül 4
Mis on geomeetria?
Õpetaja esitab õpilastele küsimuse ja õpilased vastavad oma sõnadega.
Geomeetria
Geomeetria (kreeka keeles, maamõõdukunst) on matemaatika haru, mis käsitleb geomeetrilisi kujundeid, st kehi, pindu, jooni ja punkte. Geomeetria algeid leidub seoses maamõõtmise, planeerimise jt toimingutega Egiptuse ja Babüloonia matemaatiliste ülesannete tekstides juba 2000. a eKr.
Geomeetrilisi kujundeid liigitatakse tasandilisteks ja ruumilisteks. Tasandil paiknevaid kujundeid uurivat haru nimetatakse planimeetriaks. Ruumis paiknevaid kujundeid uurivat haru nimetatakse stereomeetriaks.
Ajurünnak: milliseid geomeetrilisi kujundeid sa tead?
Õpetaja jaotab tahvli pooleks ja kirjutab ühele poolele pealkirjaks „Tasandilised kujundid“ ja teisele poolele „Ruumilised kujundid“. Õpilased teevad samasuguse tabeli oma vihikusse. Seejärel arutatakse koos, kuidas aru saada, kas kujund on tasandiline või ruumiline.
Distantsõpe
Õpilased lahendavad ptk 6.1 ül 1, kus tuleb otsustada, kas geomeetriline kujund on tasandiline või ruumiline.
Pärast arutelu kirjutab iga õpilane vihikusse talle tuttavate kujundite nimetusi. Selleks võiks anda aega umbes 3 minutit.
Seejärel kutsub õpetaja järjest õpilasi tahvli juurde ja iga õpilane saab kirjutada tahvlil olevasse tabelisse ühe kujundi nimetuse.
Kui õpilased on kõik neile meenunud kujundite nimetused ära kirjutanud, kuvab õpetaja ekraanile pildi geomeetrilistest kujunditest.
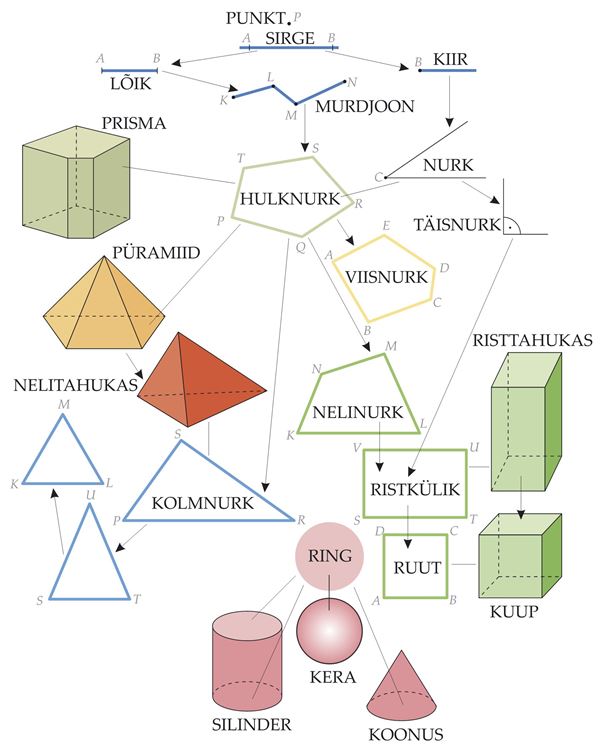
Koos vaadatakse, millist kujundit õpilased tabelisse ei kirjutanud. Õpilased täiendavad tabelit nii tahvlil kui ka oma vihikus.
Arutelu: kuidas on kujundid omavahel seotud?
Pildil olevat skeemi uurides saab õpilastega arutleda, kuidas on kujundid omavahel seotud, mis on neis erinevat, mis ühist, mida tähendavad nooled skeemil.
Abistavaid küsimusi aruteluks
Küsimus | Vastus | |
1. | Mille poolest erinevad lõik, kiir ja sirge? | Lõigul on 2 otspunkti, kiirel 1 ja sirgel ei olegi otspunkte. |
2. | Kuidas tekib nurk? | Nurga moodustavad kaks ühest ja samast punktist väljuvat kiirt. |
3. | Kuidas tekib murdjoon, kuidas hulknurk? | Murdjoon koosneb lõikudest. Hulknurk on murdjoonega piiratud kinnine kujund. |
4. | Kas kolmnurgad ja nelinurgad on hulknurgad? | Jah. |
5. | Kas ristkülikuid võib nimetada ka nelinurkadeks? | Jah. |
6. | Kas igat nelinurka võib nimetada ristkülikuks? | Ei või. |
7. | Mille poolest erineb ristkülik tavalisest nelinurgast, ruut ristkülikust? | Ristkülikul on vastasküljed võrdsed ja paralleelsed ning kõik nurgad on täisnurgad, aga nelinurgal ei pea olema. Ruudul on kõik küljed võrdsed ja kõik nurgad on täisnurgad. |
8. | Kas ruut on ka ristkülik? | Ruut on võrdsete külgedega ristkülik. |
9. | Kas kuup on ka risttahukas? | Kuup on risttahukas, mille tahkudeks on ruudud. |
10. | Kuidas on ring seotud kera, silindri ja koonusega? | Ring on silindri ja koonuse põhjaks ning kera läbilõikeks. |
11. | Kas kõik tasandilised kujundid on hulknurgad? | Ei ole (nt punkt, sirge, kiir, lõik, nurk). |
Punkt
Punkt on kõige väiksem geomeetriline kujund, sel ei ole pikkust ega laiust, seda ei saa mõõta.
Punkte tähistatakse matemaatikas suurte tähtedega (A, B, C jne), sirgeid väikeste tähtedega (a, b, c jne).
Distantsõpe
Õpilased lahendavad ptk 6.1 ül 2–4.
Pärast arutelu lahendavad õpilased iseseisvalt ptk 6.1 ül 2 ja 3.
Ümbermõõdu, pindala ja ruumala valemid
Koos tuletatakse meelde ka õpitud ümbermõõdu, pindala ja ruumala valemid.
Seejärel lahendavad õpilased iseseisvalt ptk 6.1 ül 4.
Hulknurgad
25
- Animatsioonide vaatamine (hulknurk; ristküliku ja ruudu ümbermõõt)
- Hulknurga ümbermõõdu leidmine
- Liikumisharjutus (tõene/väär)
Animatsioonide vaatamine (hulknurk; ristküliku ja ruudu ümbermõõt)
Õpilased on varem tutvunud hulknurgaga ja õppinud arvutama hulknurga ümbermõõtu. Selle meeldetuletamiseks võib vaadata kahte animatsiooni.
Hulknurga kõigi külgede summa on tema ümbermõõt.
Hulknurga ümbermõõdu leidmine
Õpetaja kuvab ekraanile kujundi ja palub õpilastel mõelda, kuidas saab leida ekraanil oleva kujundi ümbermõõtu.
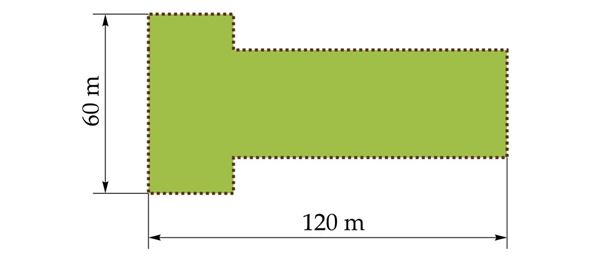
Õpilased võivad alguses arutada koos paarilisega ja seejärel palub õpetaja kellelgi selgitada oma lahendust.
Vajaduse korral võib õpetaja joonise abil ise lahendust selgitada.
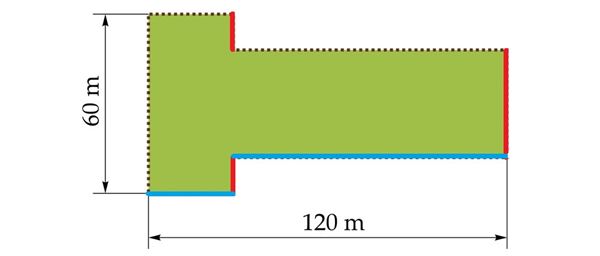
Liikumisharjutus (tõene/väär)
Õpilased seisavad klassi keskele. Õpetaja ütleb, et klassi üks sein (nt paremal käel) kannab nime Tõene ja vastassein (nt vasakul käel) nime Väär. Õpetaja hakkab ekraanile kuvama lauseid. Õpilane peab otsustama, kas lause on tõene ja väär ning liikuma seejärel vastava seina juurde. Kui keegi vastab valesti, siis tuleks lühidalt selgitada, miks see lause on õige või vale. Pärast igat lauset tulevad õpilased tagasi klassi keskele.
Distantsõpe
Õpetaja saadab õpilastele ptk 6.1 ülesannete kogust tõesed/väärad laused nutiseadmes lahendamiseks.
Ümbermõõdu, pindala ja ruumala arvutamine
15
- 8 ülesande lahendamine. Opiq ül 6, 7
- Lisaülesanne kiirematele, Opiq ül 8
- Vastuste kontrollimine
8 ülesande lahendamine
Õpilased istuvad tagasi oma kohale ja avavad vihikud. Õpetaja hakkab ekraanil näitama ülesandeid. Iga ülesande lahendamiseks on aega 1–2 minutit. Õpilased kirjutavad vihikusse andmed, tehted ja arvutavad nõutud suuruse. Kui mõni õpilane ei jõua etteantud ajaga ülesannet lahendada, siis võib lasta tal pärast oma arvutused lõpetada. Teised lahendavad samal ajal lisaülesande.
Soovi korral võivad õpilased lahendada samad ülesanded ptk 6.1 (ül 5, 6) või annab õpetaja õpilastele töölehe.
Vastuste kontrollimine
Pärast kaheksa ülesande lahendamist kontrollivad õpilased ise oma vastused ja annavad hinnangu oma tööle. Õpetaja kuvab õiged vastused ekraanil.
Lahendused õpetajale

Kokkuvõte
15
- Oskuste bingo
Õpetaja on enne tundi välja printinud bingokaardid.
Oskuste bingo
Iga õpilane saab ühe kaardi, kus on tabelis kirjas erinevad oskused. Tabeli keskmisse ruutu kirjutab õpilane oma nime. Seejärel liiguvad õpilased klassis ringi ja püüavad välja selgitada, kes mida oskab. Iga oskuse juurde on vaja kirjutada ühe õpilase (või õpetaja) nimi, kusjuures ühe ja sama õpilase nime ei tohi mitmesse kohta kirjutada. Õpetaja nime kirjutamise vajadus tekib ilmselt ringi pindala ja ümbermõõdu juurde, kuna seda pole õpilased veel õppinud.
Kes saab tabeli nimedega täidetud, hüüab „Bingo“ ja tuleb seisab tahvli juurde.
Kui kõik on ülesande täitmise lõpetanud, korjab õpetaja kaardid kokku. Seejärel ta selgitab, millised vahendid on vaja kaasa võtta järgmiseks tunniks.
Kodutöö ja tunni kirjeldus
Kodutöö
Tunni kirjeldus
Kordamine. Geomeetrilised kujundid. Pindala, ümbermõõdu ja ruumala valemid ning nende abil arvutamine |
Opiq ptk 6.1 |
