(Математика 7)

Что такое рациональные числа? Что нового мы изучим?

Мы встречаемся с числами повсюду. Каждый день нам приходится что-нибудь подсчитывать, измерять и вычислять. Вспомни, что ты сегодня подсчитал, измерил или вычислил.

Числа 0; 1; 2; 3; ... называются натуральными числами. Ими ты наверняка пользовался до того, как начал ходить в школу, но познакомился с их свойствами только в начальных классах. Натуральные числа всегда можно складывать и перемножать, но при вычитании или делении не всегда получается натуральноое число.

Для того, чтобы можно было вычесть из меньшего числа большее, вводят отрицательные числа, то есть числа, противоположные натуральным. Выполнять действия с этими числами ты научился в предыдущем учебном году. Натуральные числа и им противоположные числа вместе образуют множество целых чисел.

Для того, чтобы всегда стало возможным деление двух целых чисел (кроме деления на нуль), нужно ввести положительные и отрицательные дробные числа. Дробные и целые числа вместе образуют множество рациональных чисел. В этой главе мы научимся выполнять действия с рациональными числами.

Усвоив материал этой главы, ты будешь знать, что означают выражения:

рациональное число,

противоположное число,

модуль числа,

степень числа,

а также будешь уметь:

упорядочивать рациональные числа;
складывать, вычитать, умножать и делить эти числа;
пользоваться правилами порядка выполнения действий, а также законами сложения и умножения;
вычислять расстояние между двумя точками числовой оси;
вычислять значения буквенных выражений, содержащих рациональные числа;
возводить числа в степень;
пользоваться степенями числа 10 для записи очень больших чисел;
решать текстовые задачи и простейшие уравнения.

Lisää aiheesta

ВВОДНОЕ ПОВТОРЕНИЕ И ДОПОЛНЕНИЯ

За лето ты, наверно, успел подзабыть кое-что из ранее изученного. Поэтому прежде, чем изучать новый материал, тебе следует освежить в памяти свои знания.

A()

B()

C()

D()

E()

G()

–87
–23
15
–5,2
3,8
–14
14
100
–7
23
–0,1
–27

Числа	Расстояние до начала отсчета	Направление
$\|5\|$	единиц
$\|- 6\|$	единиц
$- \|- 2\|$	единицы
$0, 7$	единицы
$- \|1, 2\|$	единицы
$- \|\frac{5}{6}\|$	$\frac{}{}$ единицы
$\|- \frac{5}{8}\|$	$\frac{}{}$ единицы
$\|0, 12\|$	единицы
$\|0\|$	единиц

–7 < 1

, , , , , ,

–2 < 5

, , , , ,

–7 < –1

, , , ,

–2,5 < 3,8

, , , , ,

–100,3 < –95,2

, , , ,

10 – 15 =

–25 + 15 =

–6 + (–7) =

–6 – 7 =

–21 – (–30) =

25 · (–3) =

–15 · 20 =

–12 · (–10) =

–14 · 15 =

11 · (–12) =

–42 : 14 =

75 : (–25) =

–36 : 18 =

–60 : (–10) =

42 : (–3) =

25 · (–2) – 49 =

–36 : 4 – 7 =

–3 · (6 – 10) – 12 =

56 : (–7) + 9 =

12 – 8 : 2 =

2 + (–7) – 12 – (–8) + 10 – 11 =

15 – 10 + 25 + 12 – 25 – 10 – 100 =

–14 – 6 – 25 + 40 + 25 – 20 =

125 – 25 + 28 + 52 – 16 – 4 + 95 =

Значение буквы	Значение буквенного выражения
n = –10	=
n = 50	=

Значение буквы	Значение выражения
m = –10	=
m = 5	=

x + 7 = 28
x =

t + 10 = –1
t =

10 – x = 7
x =

–10 – x = 7
x =

3t = 6
t =

–4t = 8
t =

2x = –10
x =

–3x = –9
x =

2n + 4 = 8
n =

2n + 6 = –10
n =

2x – 5 = 1
x =

2x – 6 = –4
x =

1) \|x\| = 5
2) \|x\| = 10
3) \|x\| = –5

4) –\|x\| = –10
5) \|–x\| = 2
6) \|–x\| = –1

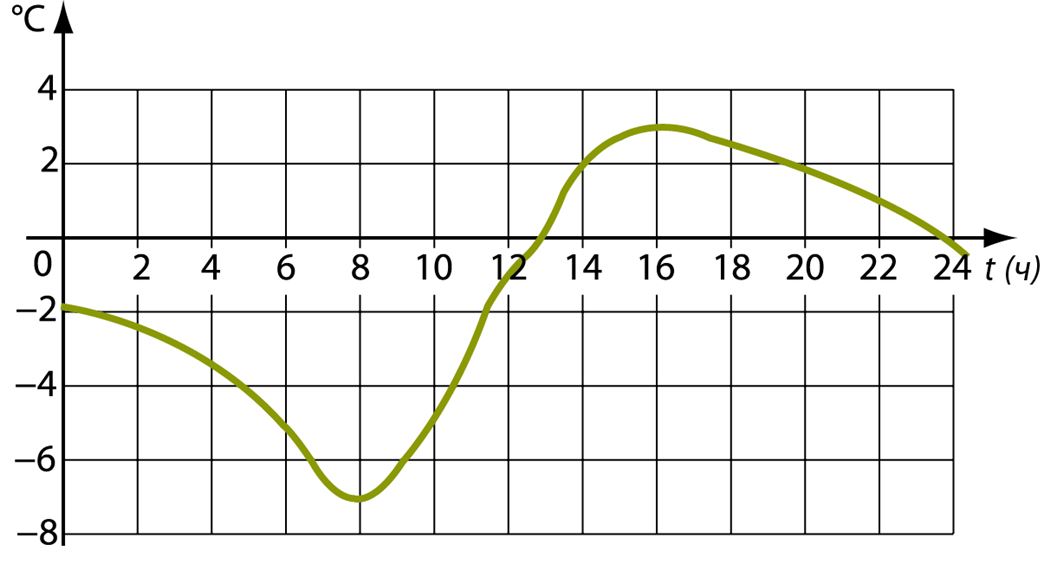
Определи по графику:

1) какую температуру показывал термометр

в 3.00?	в 12.00?	в 20.00?	в 5.30?
℃	℃	℃	℃

2) в какое время температура была –3°, 0°, +2°;

–3° была в  и в  ,
0° была в  и в ,
+2° была в  и в .

3) в какое время температура была самой низкой и сколько это было градусов;

Самая низкая температура была в и составляла ℃.

4) в какое время температура была самой высокой и сколько это было градусов;

Самая высокая температура была в и составляла ℃.

5) в какой промежуток времени термометр показывал температуру ниже нуля и в какой промежуток времени – выше нуля;

Термометр показывал температуру ниже нуля с

до , а температуру выше нуля с до .

6) как изменялась температура в промежутке времени

с 10 ч до 15 ч

с 2 ч до 8 ч

7) в какие промежутки времени температура понижалась, в каком промежутке повышалась.

Температура понижалась с до и с до , а понижалась с до .

$\frac{16}{20}$ = $\frac{}{}$

$\frac{9}{12}$ = $\frac{}{}$

$\frac{21}{35}$ = $\frac{}{}$

$\frac{13}{26}$ = $\frac{}{}$

$\frac{25}{75}$ = $\frac{}{}$

$\frac{36}{30}$ = $\frac{}{}$

$\frac{55}{100}$ = $\frac{}{}$

$\frac{3}{4}$ и $\frac{1}{6}$

$\frac{3}{4}$ = $\frac{}{}$

$\frac{1}{6}$ = $\frac{}{}$

$\frac{3}{4}$ $\frac{1}{6}$

$\frac{2}{7}$ и $\frac{5}{14}$

$\frac{2}{7}$ = $\frac{}{}$

$\frac{5}{14}$ = $\frac{}{}$

$\frac{2}{7}$ $\frac{5}{14}$

$\frac{7}{12}$ и $\frac{5}{18}$

$\frac{7}{12}$ = $\frac{}{}$

$\frac{5}{18}$ = $\frac{}{}$

$\frac{7}{12}$ $\frac{5}{18}$

$\frac{11}{20}$ и $\frac{13}{30}$

$\frac{11}{20}$ = $\frac{}{}$

$\frac{13}{30}$ = $\frac{}{}$

$\frac{11}{20}$ $\frac{13}{30}$

57 + 203 =

3002 – 9 =

195 + 405 =

128 – 38 =

0,8 – 0,25 =

1,24 + 3,06 =

2,74 – 1,7 =

3,8 + 6,2 =

4 · 205 =

2408 : 4 =

30 · 15 =

6000 : 20 =

1,6 : 4 =

0,8 · 0,05 =

0,2 : 0,01 =

1,6 : 0,8 =

$\frac{4}{7}$ + $\frac{3}{7}$ = $\frac{}{}$ =

$\frac{10}{11}$ – $\frac{5}{11}$ = $\frac{}{}$

$\frac{3}{5}$ + $\frac{1}{5}$ = $\frac{}{}$

$\frac{8}{15}$ – $\frac{1}{5}$ = $\frac{}{}$ = $\frac{}{}$

$\frac{12}{13}$ – $\frac{7}{13}$ = $\frac{}{}$

$\frac{8}{9}$ + $\frac{4}{9}$ = $\frac{}{}$ = $\frac{}{}$

3 – $\frac{2}{3}$ = $\frac{}{}$

$\frac{1}{2}$ + $\frac{1}{5}$ = $\frac{}{}$

$\frac{2}{3}$ ⋅ $\frac{1}{5}$ = $\frac{}{}$

$\frac{4}{5}$ : 3 = $\frac{}{}$

6 ⋅ $\frac{1}{6}$ =

4 : $\frac{1}{4}$ =

$\frac{3}{5}$ : $\frac{3}{4}$ = $\frac{}{}$

$\frac{5}{6}$ ⋅ $\frac{3}{5}$ = $\frac{}{}$

2 : $\frac{2}{3}$ =

$\frac{3}{10}$ ⋅ 5 = $\frac{}{}$ = $\frac{}{}$

$\frac{33}{100}$ =

$\frac{4}{5}$ =

$\frac{3}{10}$ =

$\frac{5}{8}$ =

2 $\frac{3}{4}$ =

1 $\frac{4}{25}$ =

3 $\frac{21}{50}$ =

0,7 = $\frac{}{}$

1,25 = $\frac{}{}$

0,36 = $\frac{}{}$

2,04 = $\frac{}{}$

0,65 = $\frac{}{}$

3,47 = $\frac{}{}$

1,205 = $\frac{}{}$

0,5 + $\frac{1}{3}$ =

$\frac{4}{5}$ – 0,3 =

$\frac{7}{12}$ + 0,25 =

1 $\frac{1}{2}$ – 0,15 =

3,6 + $\frac{5}{6}$ =

2 $\frac{3}{4}$ – 2,65 =

0,4 : $\frac{4}{15}$ =

$\frac{1}{6}$ ⋅ 0,45 =

$\frac{3}{8}$ : 1,25 =

$\frac{7}{12}$ ⋅ 0,9 =

3 $\frac{2}{5}$ : 0,17 =

5,1 : $\frac{3}{10}$ =

984 + 3926 =

4000 – 598 =

195 + 14 866 =

95 041 – 8704 =

4,807 + 0,39 =

5,1 – 2,88 =

3,06 – 0,158 =

15,4 + 38,63 =

47 · 529 =

7740 : 36 =

604 · 105 =

10 452 : 52 =

9,477 : 2,7 =

0,84 · 3,5 =

0,0704 : 0,11 =

0,61 · 1,12 =

Вычисли среднюю скорость $(\frac{км}{ч}),$ округлив ответ до десятых.

Ответ: Средняя скорость победителя была $\frac{км}{ч}$ .

Сколько полных оборотов сделало за время гонки переднее колесо велосипеда победителя, если диаметр колеса был 1,27 м? Ответ округли до тысяч.

Ответ: на этом пути переднее колесо велосипеда сделало примерно полных оборотов.

Сравни диаметр этого колеса с диаметрами колес современных велосипедов.

Рудольф Льюис

$\frac{1}{2}$ = %

$\frac{3}{4}$ = %

$\frac{9}{10}$ = %

0,35 = %

0,08 = %

$\frac{8}{100}$ = %

0,0045 = %

0,023 = %

Процент	Десятичная дробь	Обыкновенная дробь
30%		$\frac{}{}$
45%		$\frac{}{}$
67%		$\frac{}{}$
80%		$\frac{}{}$

Процент	Десятичная дробь	Обыкновенная дробь
100%		$\frac{}{}$
85%		$\frac{}{}$
22%		$\frac{}{}$
48%		$\frac{}{}$

(100; 10)	= %
(500; 25)	= %
(120; 12)	= %
(60; 4)	= %
(1200; 240)	= %

Ответ: природный парк занимает % всей возвышенности Отепя.

Ответ: площадь треугольника равна см².

1) 0, 3, 2, 5, 4, 7, 6, 9, , , ...

2) 3, 1, 4, 2, 5, 3, 6, 4, , , ...

Lisää aiheesta

Edistyminen

	Tehtävät
	Luku on suoritettu

Что такое рациональные числа? Что нового мы изучим?

Lisää aiheesta

ВВОДНОЕ ПОВТОРЕНИЕ И ДОПОЛНЕНИЯ

Lisää aiheesta

Lisää materiaali

Lisättävät tiedostot

Ilmoita virheestä

Ilmoita tänne vain alustaan ja sisältöön liittyvistä virheistä. Pyydämme kuvailemaan virhettä mahdollisimman tarkasti.

Liitä halutessasi mukaan yhteystietosi (sähköpostiosoite, puhelin).

Tee rasti ruutuun, näin autat meitä taistelussa roskapostia vastaan

Opiq käyttää evästeitä