Funktsiooni piirväärtus

Jada piirväärtus
Piirväärtuse mõiste
Piirväärtuse täpsem definitsioon
Lõpmatu piirväärtus
Piirväärtust ei eksisteeri

Jada piirväärtus

Meenuta

Kui jada {a_n} liikmed a_n erinevad n-i kasvades üha vähem ja vähem konkreetsest väärtusest a, siis öeldakse, et arv a on jada {a_n} piirväärtus, kui n läheneb lõpmatusele.

$\lim_{n \to \infty} a_{n} = a$

Jada piirväärtus saab olla lõplik või lõpmatu.
Jadal võib piirväärtus puududa.

$\lim_{n \to \infty} {(- 5)}^{n} =$
$\lim_{n \to \infty} \frac{2}{n^{2}} =$
$\lim_{n \to \infty} \frac{n^{3}}{3 n - 3} =$
$\lim_{n \to \infty} \frac{10 n}{n + 5} =$
$\lim_{n \to \infty} \frac{n + 5}{n} =$

Lisää aiheesta

Piirväärtuse mõiste

Funktsiooni piirväärtus

Arv a on funktsiooni f (x) piirväärtus argumendi x lähenemisel x₀-le, kui funktsiooni väärtuse erinevus arvust a on kui tahes väike, eeldusel, et argument x on piisavalt lähedal kohale x₀.

Märka

Kui argument x läheneb x₀-le ja funktsiooni f (x) väärtuste erinevus arvust a läheneb nullile, siis a on funktsiooni f (x) piirväärtus.

$\lim_{x \to x_{0}} f (x) = a$

Näide 1

Põhjendame arvutustega, et $\lim_{x \to 2} (0,5 x^{2} - 1) = 1 .$

Lahendus

Läheneme kohale x₀ = 2. Selleks moodustame kaks arvjada, mille piirväärtus on 2.
1. a_n = 2 – 0,5ⁿ, n ∈ ℕ
2. b_n = 2 + 0,5ⁿ, n ∈ ℕ
Uuri joonist 1, kus funktsiooni f (x) graafikul liiguvad kaks punkti, mille
1. abstsissid on jadade liikmed a_n ja b_n,
2. ordinaadid on funktsiooni väärtused f (a_n) ja f (b_n).
Näeme, et mida vähem jada liige a_n või b_n erineb kahest, seda vähem erineb funktsiooni vastav väärtus f (a_n) või f (b_n) arvust a = 1. Seega võib eeldada, et eksisteerib piirväärtus

$\lim_{x \to 2} (0,5 x^{2} - 1) = 1 .$

Joonis 1

Lisää aiheesta

Piirväärtuse täpsem definitsioon

Definitsioon

Arv a on funktsiooni f (x) piirväärtus argumendi x lähenemisel x₀-le, kui mis tahes väikese positiivse arvu ε > 0 jaoks leidub selline δ (ε) > 0 (mis sõltub ε-st), et

|x – x₀| < δ(ε) ⇒|f (x) – a| < ε,

kusjuures x ≠ x₀.

Märka

|f (x) – a| on funktsiooni väärtuse erinevus piirväärtusest a.
|x – x₀| on argumendi x erinevus kohast x₀.
Tingimus x ≠ x₀ on vajalik seetõttu, et funktsioon y = f (x) ei pruugi olla määratud kohal x₀ või x₀, mis on katkevuskoht.

Näide 2

Näitame definitsiooni põhjal, et $\lim_{x \to 2} (2 x - 3) = 1 .$

Lahendus

Mis tahes ε > 0 korral peab leiduma δ (ε) > 0, et

|x – 2| < δ (ε) ⇒|2x – 3 – 1| < ε.

Lahendame võrratuse |2x – 4| < ε.

|2(x – 2)| < ε

$|x - 2| < \frac{ε}{2}$

Järelikult saame võtta $δ (ε) < \frac{ε}{2}$ või mingi väärtuse, mis on sellest väiksem, näiteks $\frac{ε}{3} .$

Joonis 2

Üldisem selgitus

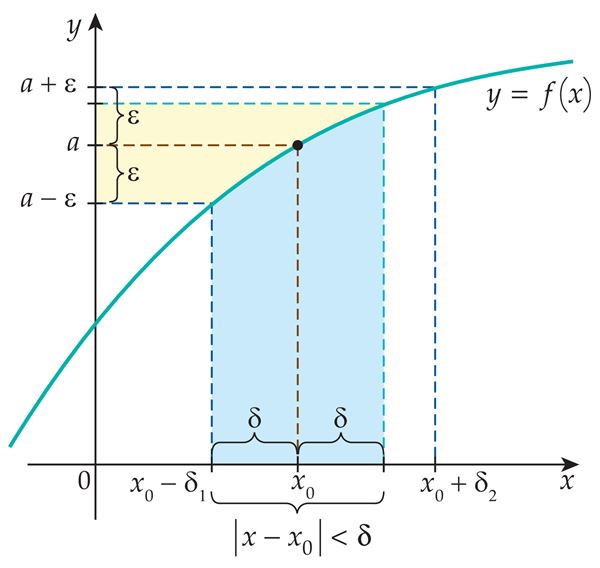
Jooniselt 3 on näha, et võrratus |f (x) – a| < ε on täidetud, kui argument x asub vahemikus

X₁ = (x₀ – δ₁; x₀ + δ₂).

Definitsiooni kohaselt peab leiduma selline δ (ε), et

|x – x₀| < δ(ε)
ehk
x₀ – δ (ε) < x < x₀ +δ (ε).

See vahemik peab seega asuma vahemiku X₁ sees. Järelikult on suurimaks võimalikuks δ (ε) väärtuseks

δ = min{δ₁ ; δ₂}.

Joonis 3

Lisää aiheesta

Lõpmatu piirväärtus

Lähenemine lõpmatusele

Arv a on funktsiooni f (x) piirväärtus argumendi x lähenemisel pluss lõpmatusele, kui funktsiooni väärtus erineb arvust a kui tahes vähe, eeldusel, et argument x on piisavalt suur.

$\lim_{x \to \infty} f (x) = a$

Arv a on funktsiooni f (x) piirväärtus argumendi x lähenemisel miinus lõpmatusele, kui funktsiooni väärtus erineb arvust a kui tahes vähe, eeldusel, et argument x on piisavalt väike (negatiivne).

$\lim_{x \to - \infty} f (x) = a$

Märka

Nii nagu jada korral, võib ka funktsiooni piirväärtus olla lõplik, lõpmatu või üldse mitte eksisteerida.

Lõpmatu piirväärtus

Piirväärtus pluss lõpmatus

Funktsiooni f (x) piirväärtus on pluss lõpmatus argumendi x lähenemisel x₀-le, kui funktsiooni väärtus on kui tahes suur, eeldusel, et x on piisavalt lähedal x₀-le.

$\lim_{x \to x_{0}} f (x) = + \infty$

Piirväärtus miinus lõpmatus

Funktsiooni f (x) piirväärtus on miinus lõpmatus argumendi x lähenemisel x₀-le, kui funktsiooni väärtus on kui tahes väike (negatiivne), eeldusel, et x on piisavalt lähedal x₀-le.

$\lim_{x \to x_{0}} f (x) = - \infty$

Märka katkevuskohta

Kui funktsiooni väärtus kasvab (või kahaneb) tõkestamatult argumendi x lähenemisel x₀-le, siis x₀ on funktsiooni katkevuskoht.

Näide 3

Näitame, et $\lim_{x \to 1} \frac{1}{{(x - 1)}^{2}} = + \infty .$

Peame näitama, et funktsiooni $y = \frac{1}{{(x - 1)}^{2}}$ väärtus on suurem kui tahes suurest arvust A > 0, kui x on piisavalt lähedal kohale 1.
Lahendame võrratuse $\frac{1}{{(x - 1)}^{2}} > A > 0 .$

${(x - 1)}^{2} < \frac{1}{A} \Leftrightarrow |x - 1| < \frac{1}{\sqrt{A}},$ sest

$\sqrt{{(x - 1)}^{2}} = |x - 1| .$

Näeme, et kui x on kohale 1 lähemal kui $δ = \frac{1}{\sqrt{A}},$ on funktsiooni väärtus suurem mis tahes arvust A > 0.
Järelikult eksisteerib lõpmatu piirväärtus

$\lim_{x \to 1} \frac{1}{{(x - 1)}^{2}} = + \infty .$

Joonis 4

Lisää aiheesta

Piirväärtust ei eksisteeri

Näide 4

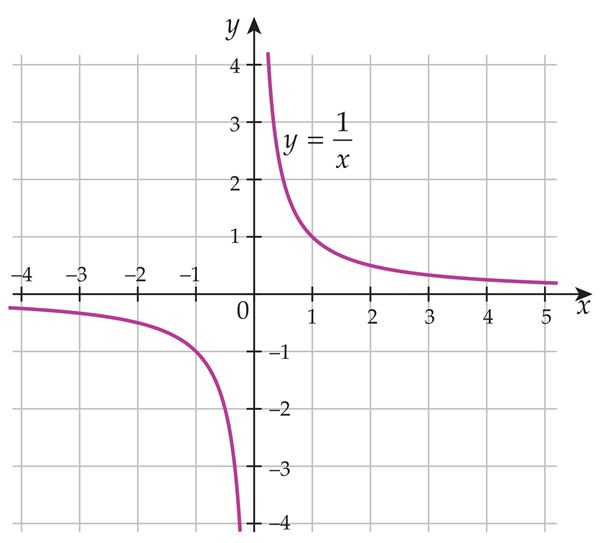
Näitame, et $\lim_{x \to 0} \frac{1}{x}$ ei eksisteeri.

Kui x läheneb nullile, siis murd 1x läheneb lõpmatusele.
1. Kui x on negatiivne, siis ka $\frac{1}{x} < 0$ ja saab läheneda vaid miinus lõpmatusele.
2. Kui x on positiivne, siis $\frac{1}{x} > 0$ ja saab läheneda pluss lõpmatusele.

Kui läheneme nullile negatiivsete väärtuste poolt, saame tulemuseks miinus lõpmatuse, ja kui läheneme positiivsete väärtuste poolt, saame pluss lõpmatuse. Et märk lõpmatuse ees on erinev, siis piirväärtus

$\lim_{x \to 0} \frac{1}{x}$ puudub.

Koht x₂ = 0 on funktsiooni katkevuskoht.

Joonis 5

Märka

Piirväärtust ei eksisteeri trigonomeetriliste funktsioonide argumendi lähenemisel pluss lõpmatusele või miinus lõpmatusele.

Näide 5

Funktsiooni y = sin x väärtused muutuvad argumendi kasvades miinus ühe ja pluss ühe vahel perioodiliselt.

Seejuures pole võimalik näidata ühtegi väärtust a ( –1 ≤ a ≤ 1), millest kõik sin x väärtused erineksid näiteks vähem kui ε = 0,1 kõigi argumentide x > A korral, ükskõik kuidas me ka väärtust A ei valiks.

Sarnaselt arutledes saame näidata, et ei eksisteeri järgmised piirväärtused:

$\lim_{x \to \pm \infty} \cos x$
$\lim_{x \to \pm \infty} \tan x$
$\lim_{x \to \pm \infty} \cot x$

Lisää aiheesta

Harjuta ja treeni

Piirväärtus graafiku põhjal

$\lim_{x \to 3} (5 - 2 x) =$
$\lim_{x \to 0} (5 - 2 x) =$
$\lim_{x \to \infty} (5 - 2 x) =$

$\lim_{x \to 3} (x^{2} - 3 x + 2) =$
$\lim_{x \to 0} (x^{2} - 3 x + 2) =$
$\lim_{x \to \infty} (x^{2} - 3 x + 2) =$

$\lim_{x \to 1} (5 x - 3 x^{3}) =$
$\lim_{x \to 0} (5 x - 3 x^{3}) =$
$\lim_{x \to - \infty} (5 x - 3 x^{3}) =$

$\lim_{x \to 0} \frac{3}{x - 3} =$
$\lim_{x \to 3} \frac{3}{x - 3} =$
$\lim_{x \to \infty} \frac{3}{x - 3} =$

Lisää aiheesta

Palvelun tarjoaa Star Cloud OÜ

Rekisteröidy

Edistyminen

	Tehtävät
	Luku on suoritettu

Funktsiooni piirväärtus

Lisää aiheesta

Jada piirväärtus

Meenuta

Lisää aiheesta

Piirväärtuse mõiste

Funktsiooni piirväärtus

Märka

Näide 1

Lahendus

Joonis 1

Lisää aiheesta

Piirväärtuse täpsem definitsioon

Definitsioon

Märka

Näide 2

Lahendus

Joonis 2

Üldisem selgitus

Joonis 3

Lisää aiheesta

Lõpmatu piirväärtus

Lähenemine lõpmatusele

Märka

Lõpmatu piirväärtus

Piirväärtus pluss lõpmatus

Piirväärtus miinus lõpmatus

Märka katkevuskohta

Näide 3

Joonis 4

Lisää aiheesta

Piirväärtust ei eksisteeri

Näide 4

Joonis 5

Märka

Näide 5

Lisää aiheesta

Harjuta ja treeni

Piirväärtus graafiku põhjal

Lisää aiheesta

Lisää materiaali

Lisättävät tiedostot

Ilmoita virheestä

Ilmoita tänne vain alustaan ja sisältöön liittyvistä virheistä. Pyydämme kuvailemaan virhettä mahdollisimman tarkasti.

Liitä halutessasi mukaan yhteystietosi (sähköpostiosoite, puhelin).

Tee rasti ruutuun, näin autat meitä taistelussa roskapostia vastaan

Opiq käyttää evästeitä