(Matemaatika 6. kl)

Kordamiseks

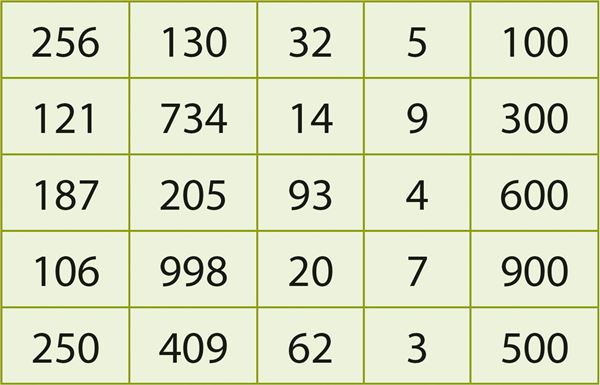
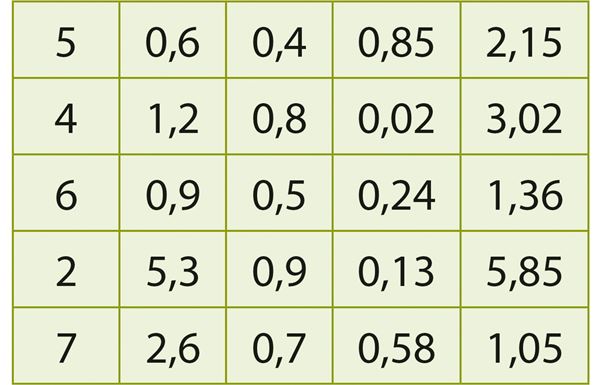
Ülesanded A

Söömine
Loodusvaatlus
Sportimine
Lugemine
Magamine
Töötamine

Loe teksti hoolega. Proovi aru saada, millisele küsimusele pead vastama.
Mõtle arvandmete üle ja otsusta, kuidas saad neid teisendada.
Teisenda arvandmed. Vasta küsimusele. Mõtle, kas sinu vastus on mõistlik.

Kümnendmurdu 0,12 loe nii:
12 sajandikku

2. Arvude lugemine

Loe arvud.

8040; $\frac{1}{2}$ ; 30 007; 0,508; $\frac{2}{3}$ ; 450 000 000; 8,02; 2 300 100 000

Mitmendik puuviljadest on pirnid?
Mitmendik õunad?
Mitmendik ploomid?

Mitmendik lastest on poisid?
Mitmendik lastest on tumeda peaga?

Mitmendik pliiatsitest on mustad?
Mitmendik pliiatsitest ei ole punased?

Mitmendik südametest ei ole värvitud?

Sellel joonisel on tervik jaotatud võrdseks osaks.

Värvimata on osa tervikust.

Sellel joonisel on tervik jaotatud võrdseks osaks.

Värvimata on osa tervikust.

Sellel joonisel on tervik jaotatud võrdseks osaks.

Värvimata on osa tervikust.

5.1 Naturaalarvudega peast liitmine-lahutamine

Liida ja lahuta (kui võimalik) kahekaupa tabeli ühes reas kõrvuti olevaid arve. Arvuta peast.

5.2 Kümnendmurdudega peast liitmine-lahutamine

Liida ja lahuta (kui võimalik) kahekaupa tabeli ühes reas kõrvuti olevaid arve. Arvuta peast.

54 310 + 23 690 =

450 760 + 1 564 768 =

86,315 + 4,085 =

478,23 + 56,09 =

1 000 000 – 24 306 =

8 607 333 – 7 970 315 =

201,1 – 7,36 =

5,062 – 1,88 =

4007 · 43 =

88 044 · 15 =

560 · 4200 =

20 · 37,5 =

0,27 · 5,9 =

1,45 · 0,97 =

1035 : 23 =

17 860 : 94 =

14 351 : 113 =

84,6 : 6 =

8,489 : 0,13 =

1,92 : 5 =

Korruta! Mitu erinevat korrutist saad?

100

2000

0,4

0,05

Jaga, kui jagajaks on ühest suurem arv.

100

0,3

0,7

64 200 – 53 609 + 1860 =

17 394 – (5682 + 473) =

0,243 : 0,3 – 0,25 · 1,08 =

51 – (3,29 · 0,1 + 6,241) =

339,52 – 129,92 – 71,35 =

207 605 – 409 · 506 =

(0,905 + 1,21 · 0,4) : 0,12 =

(49 – 38,2)(0,82 + 1,68) =

(2,3² + 0,71) : 0,3 =

(0,5 · 4³ – 26) · 1,5 =

2 · 5³ – (12² : 3 + 2) : 0,2 =

2-ga ja 5-ga jaguvuse kontrollimisel vaata arvu viimast numbrit.
3-ga ja 9-ga jaguvuse kontrollimisel liida arvu numbrid.

Arv 1 ei ole algarv ega kordarv.

Leia kordarvude kõik tegurid.
Kirjuta kordarvud alates väikseimast ning järjesta tegurid kasvavalt eraldades need komadega. Ära kirjuta tühikuid.

Arvu 18 kahekohalised kordsed on:
, , , , .

Arvu 211 kolmekohalised kordsed on:
, , , .

4 ja 18

SÜT(4;18) =

VÜK(4;18) =

12 ja 48

SÜT(12;48) =

VÜK(12;48) =

14 ja 21

SÜT(14;21) =

VÜK(14;21) =

50 ja 75

SÜT(50;75) =

VÜK(50;75) =

16 ja 100

SÜT(16;100) =

VÜK(16;100) =

Autobuss sõitis Neemelt Jõekülla 0,4 tunniga, sõiduauto aga keskmise kiirusega $75 \frac{km}{h}$ . Kumma sõiduki kiirus oli suurem ja mille võrra?

Vastus. kiirus oli $\frac{km}{h}$ võrra suurem.

Vastus. Sally kodu on koolile m lähemal kui Kadil.

Vastus. põllu ühelt hektarilt oli t võrra suurem saak.

Tähtavaldis:

Arvuta avaldise väärtus, kui x = 485 ja y = 520.

Vastus. Kare sai rooside müügist €.

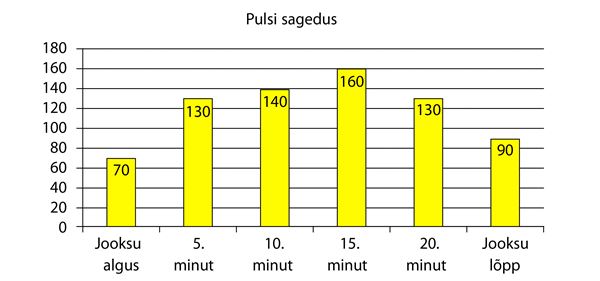
Leia diagrammilt, kui kiiresti lõi Mardi süda jooksu algul ja jooksu lõpul.
Vastus. Jooksu algul lõi Mardi süda lööki minutis ja jooksu lõpul lööki minutis.
Millal lõi Mardi süda kõige kiiremini ja kui suur oli siis pulsisagedus?
Vastus. Kõige kiiremini lõi Mardi süda ja pulsisagedus oli siis lööki minutis.
Mitme löögi võrra minutis erines Mardi pulss 15. minutil ja jooksu lõpul?
Vastus. Erinevus oli siis lööki minutis.

19. Diagramm

Lõika mõnest värskemast ajalehest välja mingi diagramm. Kleebi see oma vihikusse ja kirjuta sinna juurde, mida see diagramm kirjeldab.

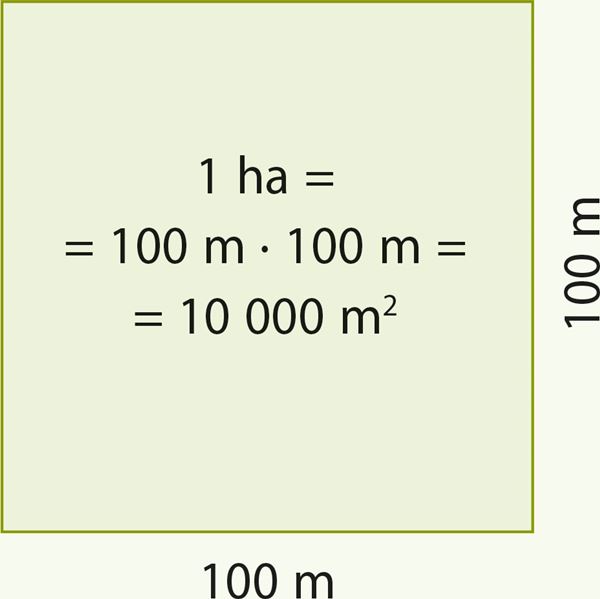1 ha on sellise ruudukujulise maatüki pindala, mille ühe külje pikkus on 100 m.

Vastus. Karjakopli pindala on ha ja ümbermõõt on km.

21. Lõik

Lõik KL = 4,5 cm.

Joonesta vihikusse

lõik MP, mis on 2,1 cm lühem lõigust KL;
lõik CD, mis on 1,2 korda pikem lõigust KL.

Vastus. Kapi ruumala on m³.

23. Nurgad

Joonesta vihikusse nurgad 55°, 90° ja 140°.

17 km = m

6,3 km = m

0,7 km = m

40 cm = m

15 cm = m

7 dm = m

4,3 dm = m

Kui 1 cm = 10 mm, siis 1 cm² = 10² mm² ja 1 cm³ = 10³ mm³.

Kui 1 dm = 10 cm, siis
1 dm² = $^{}$ cm² ja 1 dm³ = $^{}$ cm³.

Kui 1 m = 100 cm, siis
1 m² = $^{}$ cm² ja 1 m³ = $^{}$ cm³.

Jäta endale kindlalt meelde pikkusühikute vahelised seosed.
Selleks kasuta abivahendina mõõtejoonlauda.

6 ha = m²

1,8 ha = m²

0,5 ha = m²

2 km² = m²

0,4 km² = m²

700 dm² = m²

1850 dm² = m²

30 000 cm² = m²

4000 cm² = m²

4 m³ = dm³

3,2 m³ = dm³

0,2 m³ = dm³

7000 cm³ = dm³

34 000 cm³ = dm³

4,8 l = dm³

0,7 l = dm³

15 t = kg

0,45 t = kg

0,2 t = kg

6500 g = kg

94 g = kg

Ülesanded B

Joonesta vihikusse sobivad ristkülikud ning värvi murdudele $\frac{1}{5}$ , $\frac{7}{10}$ ja $\frac{21}{50}$ vastavad osad. Mida näitab iga murru nimetaja, mida lugeja?

1 657 974 : 822 · 106 – (50 377 + 20 338) =

4,32(5,67 – 2,07) + 10,53 : 4,05 – 0,152 =

(43 · 19 – 26 928 : 33)(16 112 : 53 – 304) =

4b – 3c = =

28mn – 5n + 2m = =

2(3x + 5) – 3(4x – 15) = =

Juulis ja augustis käis Neeme igal nädalal 3 korda jalgrattaga poes. Sõidukiirus oli alati keskmiselt $10 \frac{km}{h}$ . Tee võimalikud arvutused.

Vastus. sai talunik kartulite müügist € võrra rohkem raha.

Ühe auto keskmine kiirus oli $50 \frac{km}{h}$ , teisel $70 \frac{km}{h}$ . Tee võimalikud arvutused.

Tähtavaldis:

Arvuta vaalapoja kaal.

Kui x = 30, siis	vaalapoeg kaalub t.
Kui x = 100, siis	vaalapoeg kaalub t.
Kui x = 200, siis	vaalapoeg kaalub t.

Vastus. Jaanalinnu mass on korda suurem ööbiku massist ja jaanalinnu muna on korda raskem ööbiku munast.

Vastus. ∠DOE = ° või ∠DOE = °.

Vastus. Basseini täitmiseks kulub h.

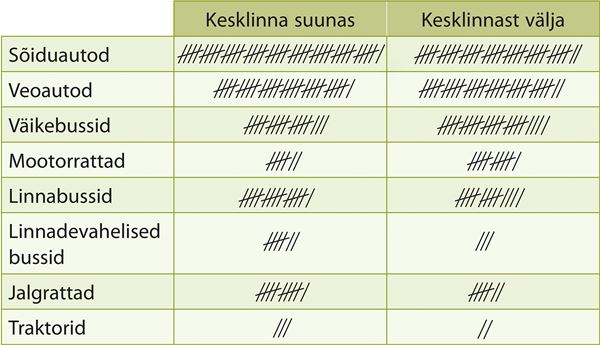
Mitu liiklusvahendit kokku sõitis kesklinna suunas ja mitu kesklinnast välja?
Vastus. Kesklinna suunas sõitis kokku liiklusvahendit ja kesklinnast välja liiklusvahendit.

Koosta nende andmete järgi diagramme.

8, 7, 6, 6, 5, 9, 10, 7, 7, 8, 3, 5, 6, 6, 7, 8, 9, 6, 6, 5, 8, 9, 7, 8, 8, 7, 7.

Koosta vihikus punktide jaotuse sagedustabel.
Leia kõigi punktide aritmeetiline keskmine.
Punktide keskmine on .
Missugune punktide arv esines kõige sagedamini?
Kõige sagedamini esines punkti.
Mitu õpilast sai kõige sagedamini esinevast tulemusest vähem punkte, mitu rohkem?
Kõige sagedamini esinevast tulemusest vähem punkte sai õpilast ja rohkem õpilast.
Koosta vihikus punktide jaotuse diagramm.

Kordamiseks

More like this

Ülesanded A

2. Arvude lugemine

5.1 Naturaalarvudega peast liitmine-lahutamine

5.2 Kümnendmurdudega peast liitmine-lahutamine

19. Diagramm

21. Lõik

23. Nurgad

More like this

Ülesanded B

More like this

Opiq score

	Tasks
	Chapter is studied

Kordamiseks

More like this

Ülesanded A

2. Arvude lugemine

5.1 Naturaal­arvudega peast liitmine-lahutamine

5.2 Kümnend­murdudega peast liitmine-lahutamine

19. Diagramm

21. Lõik

23. Nurgad

More like this

Ülesanded B

More like this

Add content

Files to be added

Report Mistake

Only report errors related to the functionality or content of Opiq. Please describe the error as precisely as possible.

If you agree to share additional info, add your contact data (e-mail, phone).

Check to help us fight spam

Opiq uses cookies

5.1 Naturaalarvudega peast liitmine-lahutamine

5.2 Kümnendmurdudega peast liitmine-lahutamine