Pärast käesoleva peatüki õppimist Sa
- tunned uusi mõisteid:
arvu ruutjuur,
ruutvõrrand,
täielik ruutvõrrand,
mittetäielik ruutvõrrand,
taandatud ruutvõrrand,
taandamata ruutvõrrand,
ruutvõrrandi diskriminant.
- tunned mõistete omadusi ja seoseid mõistete vahel:
- seos arvu ruutjuure ja absoluutväärtuse vahel;
- korrutise ruutjuur;
- jagatise ruutjuur;
- ruutvõrrandi lahendivalem;
- Viète’i teoreem.
- oskad:
- leida arvu ruutjuurt peast või taskuarvuti abil;
- leida korrutise ja jagatise ruutjuurt;
- lahendada ruutvõrrandeid ja kasutada neid tekstülesannete lahendamisel;
- kasutada ruutvõrrandi diskriminanti ning Viète’i teoreemi ruutvõrrandi lahendite uurimisel.
Arvu ruut (kordamine)
Varemõpitust teame, et kahe võrdse teguri korrutis a · a on arvu a ruut ja seda kirjutatakse lühemalt: a · a = a2. Kui a = 0, siis a2 = 0, sest 0 · 0 = 0. Kui a ≠ 0, siis a2 > 0, sest iga kahe positiivse arvu ja samuti iga kahe negatiivse arvu korrutis on positiivne.
Seega:
mis tahes ratsionaalarvu ruut on mittenegatiivne
(s.t positiivne või null).
Näide 1
52 = 5 · 5 = 25
(–1,4)2 = (–1,4) · (–1,4) = 1,4 · 1,4 = 1,96
Arvu ruudu saame leida korrutamise teel nagu näites 1. Järgnevate teemade õppimisel on kasulik arvude 1–20 ruutusid teada ka peast. Need ruudud leiad õpiku lõpus olevast lisast.
Arvu ruudu saab kergesti leida ka taskuarvuti abil. Tavaliselt on taskuarvutil selleks eriklahv x2 ja näiteks arvu 1,35 ruudu leidmiseks tuleb kasutada järgmist arvutusskeemi: 1,35 x2.
Ekraanile ilmub vastus 1,8225.
Mõnel arvutil on vaja enne arvu ruudu klahvi vajutamist vajutada veel klahvile 2nd.
Kui arvutil puudub eriklahv x2, siis tuleb toimida järgmise skeemi kohaselt: 1,35 × =.
Näide 2
Leiame 0,242 = 0,0576, järgides skeemi 0,24 × = või skeemi 0,24 x2.
(–1,7)2 = 2,89 leiame skeemi 1,7 +/– × = või 1,7 +/– x2 järgi.
Aga et (–1,7)2 = 1,72, võime selle arvutada ka nagu positiivse arvu ruudu.
–2,32 = –5,29 leiame skeemi 2,3 × = +/– või skeemi 2,3 x2 +/– järgi.
Ülesanded A
Uuri arvude 1–20 ruutude tabelit.
- Milliste numbritega lõpevad arvude 1–20 ruudud? Millise numbriga saavad lõppeda naturaalarvude ruudud, täisarvude ruudud? Millest sõltub nende arvude ruutude viimane number?
- Otsusta, millised järgmistest arvudest ei saa kindlasti olla täisarvu ruudud. Märgi need.
- 345 743
- 61 009
- 345 744
- 259 002
- 251 000
- 361 000
- 14 641
- 6477
- 10 201
- 11 236
(ab)n = an ⋅ bn
a2 − b2 = (a −b)(a + b)
=
=
=
=
- Leia selle reegli järgi
252 =
552 =
1,52 =
852 =
- Millise arvu ruut on
4225? | See on arvu ruut. |
2025? | See on arvu ruut. |
12,25? | See on arvu ruut. |
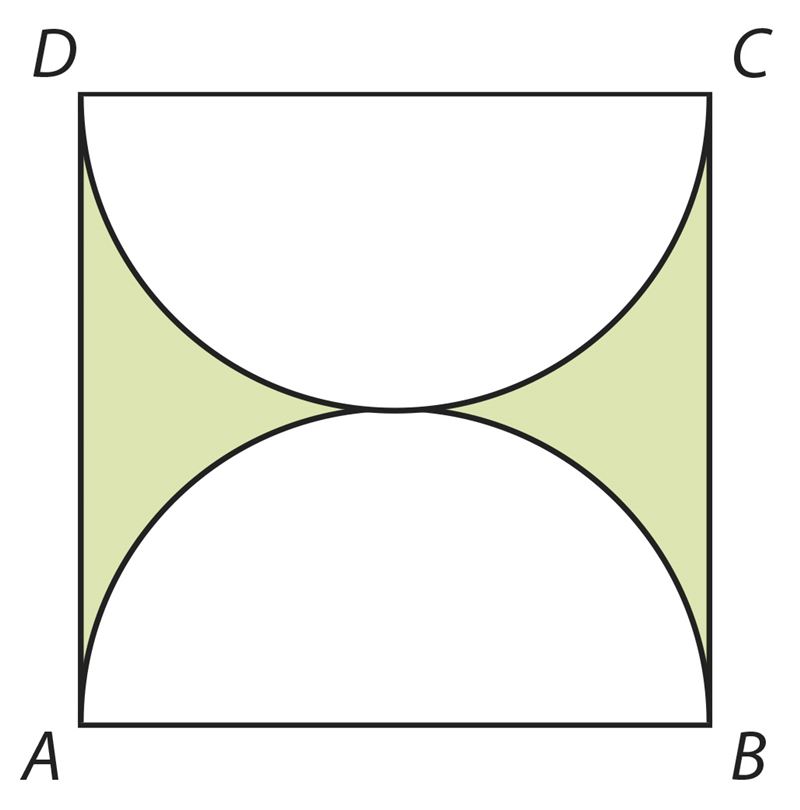
Vastus. Värvitud osa pindala moodustab ligikaudu % kogu ruudu pindalast.
Ülesanded B
- a4b4 + 4a3b3c + 4a2b2c =
Kui a = 2,4; b = 1,6; c = 2, siis avaldise väärtus on ligikaudu . - a2c2 – 2a3b2c2 + a4b4 =
Kui a = 14,6; b = 2,6; c = 9,4, siis avaldise väärtus on ligikaudu . - (a2b + b2c)(a2b – b2c) =
Kui a = 14,6; b = 0,8; c = 5,2, siis avaldise väärtus on ligikaudu .
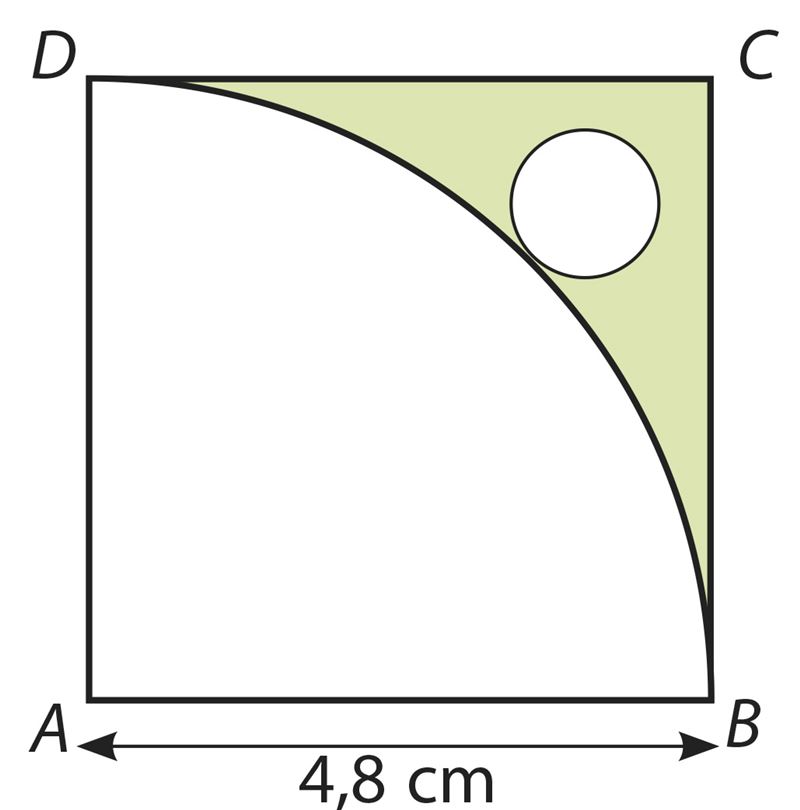
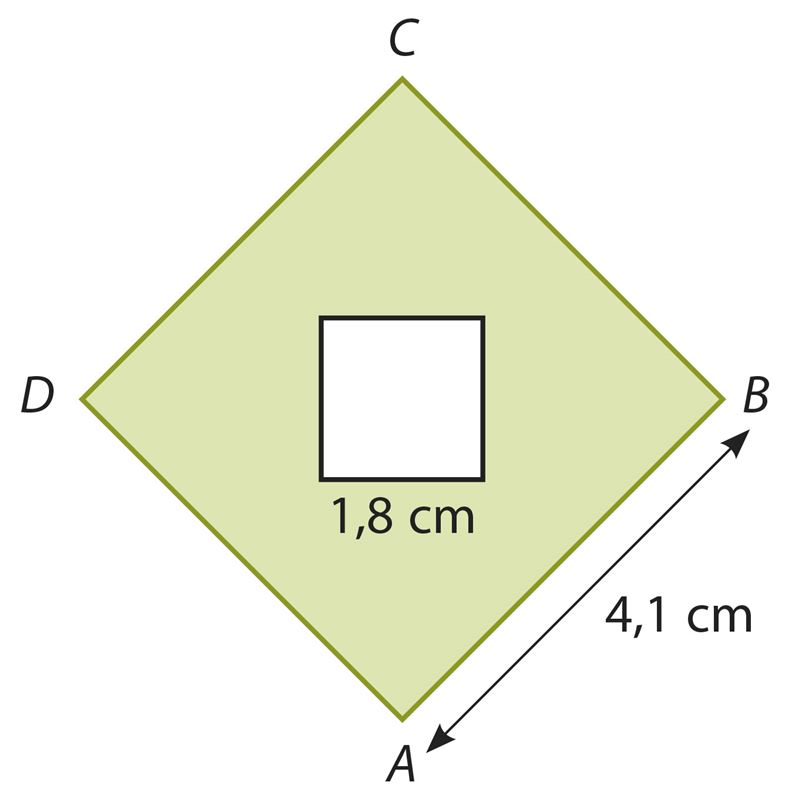
Vastus. S ≈ cm2
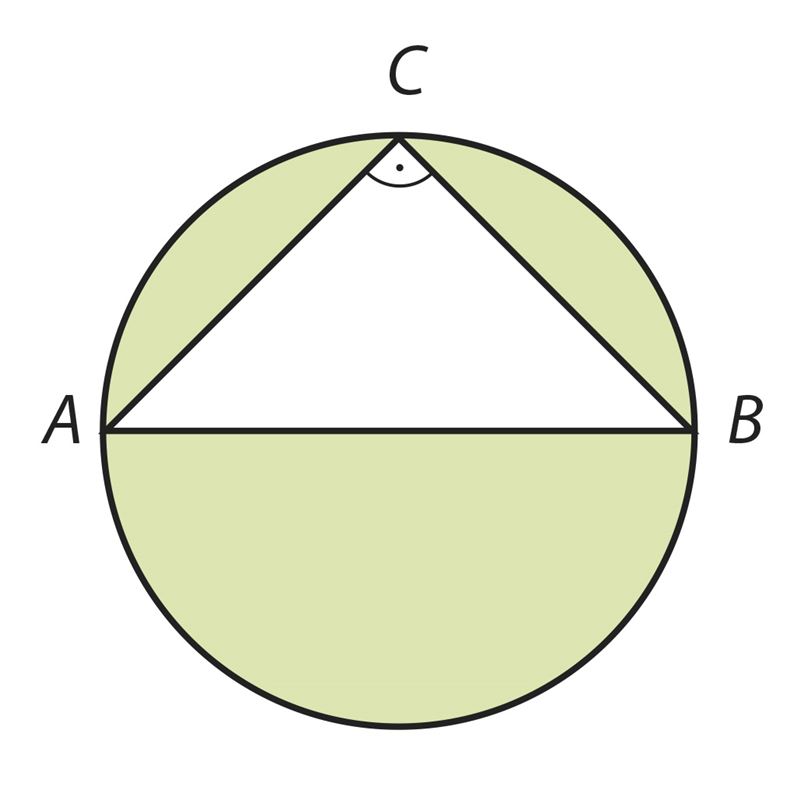
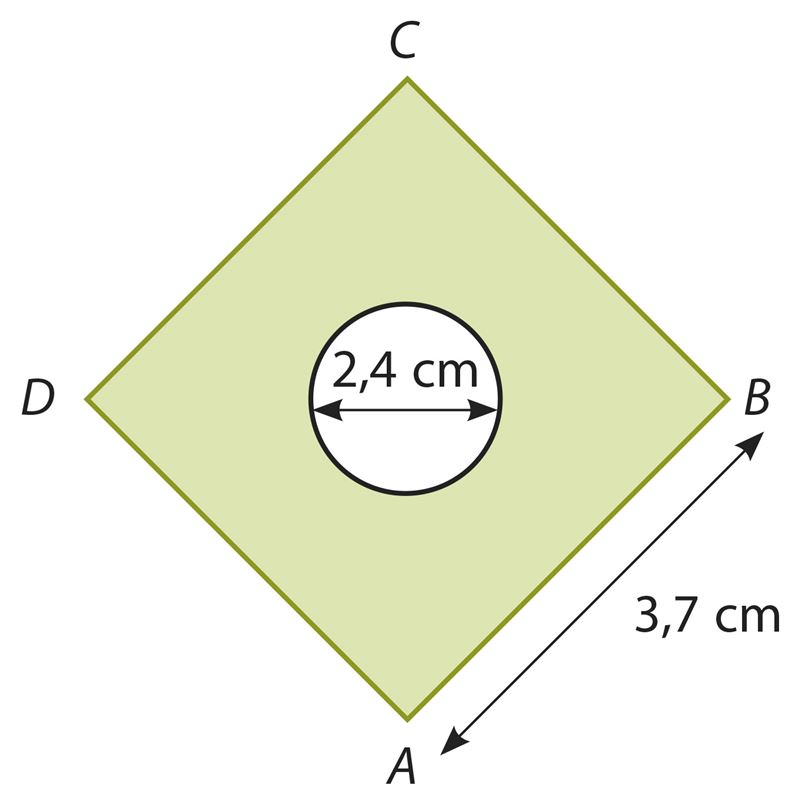
Vastus. S ≈ cm2
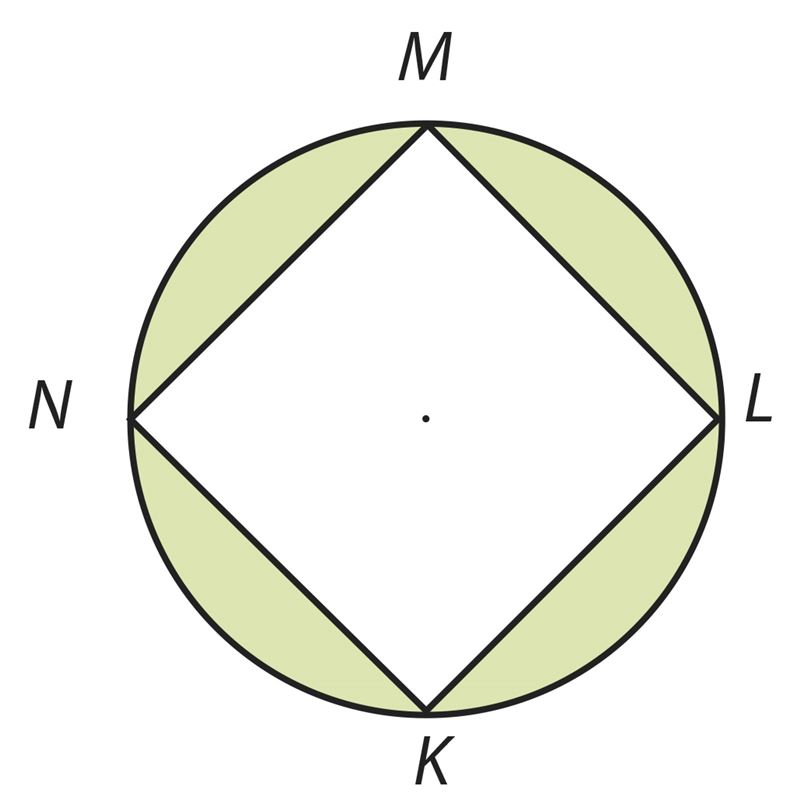
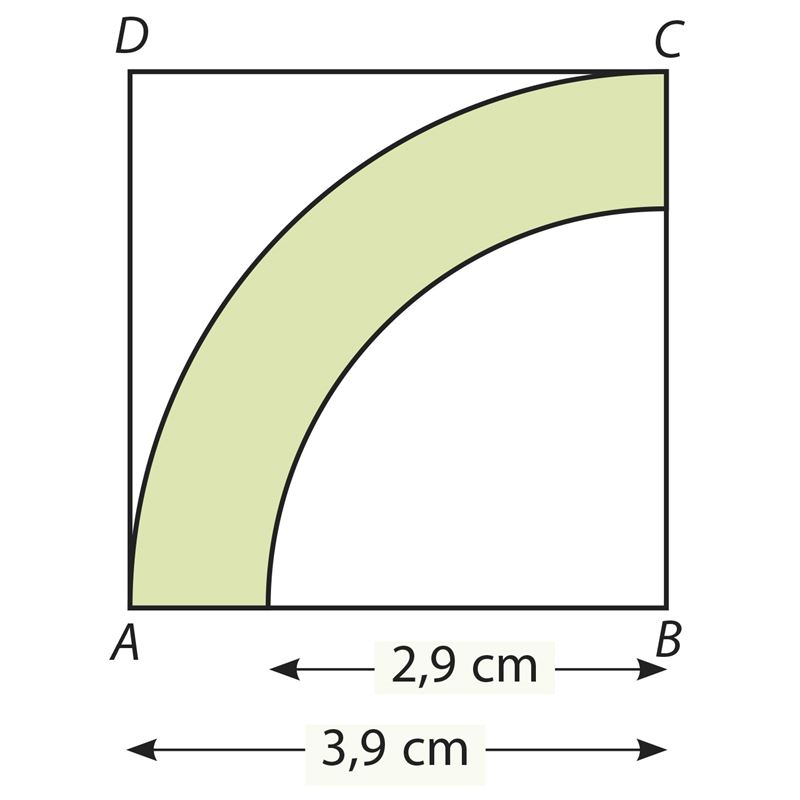
Vastus. S ≈ cm2