Eelteadmised
Õpilane
- on tutvunud eri tüüpi kaartidega ja oskab neilt teavet hankida
- oskab murdarvude väärtust võrrelda
Tunni ülesehitus
- Sissejuhatus, 2 min
- Mõõtkava, 8 min
- Kaartide jagamine mõõtkava alusel, 3 min
- Mõõtkavade võrdlemine, 15 min
- Vahemaade mõõtmine kaardil, 10 min
- Kaardi üldistamine, 6 min
- Kokkuvõte, 1 min
Eesmärgid
Õpilane
- teab, mis on mõõtkava ja saab aru, et iga kaart on maailma üldistatud mudel;
- oskab ära tunda ja eristada suuremõõtkavalist, keskmisemõõtkavalist ja väikesemõõtkavalist kaarti;
- oskab kaardil eri tüüpi mõõtkavade abil vahemaid mõõta.
Seotud materjal
Avita „Loodusgeograafia 7. klassile“
- ptk 2.4 ja selle ülesannete kogu
- ptk 2.4 (lk 20–21)
- ptk 2.4 (lk 14–15)
Märksõnad ja meetodid
- mõõtkava, suuremõõtkavaline kaart, keskmisemõõtkavaline kaart, väikesemõõtkavaline kaart, kaardi üldistamine
- töö tekstiga, harjutamine
Lõiming
Loodusõpetus 4. kl (I osa)
- ptk 2.4 „Kuidas mõõta vahemaid kaardil?“ (paberõpikus ptk 13, lk 56–59)
Matemaatika 6. kl (I osa)
- ptk 1.12 „Murdude võrdlemine (1)“ (paberõpikus ptk 5, lk 24–25)
- ptk 1.13 „Murdude võrdlemine (2)“ (paberõpikus ptk 5, lk 26–27)
Matemaatika 7. kl (II osa)
- ptk 6.1 „Võrre ja võrdekujuline võrrand“ (paberõpikus lk 23–27)
Geograafia 9. kl
- ptk 1.2 „Eesti Põhikaart. Arvutikaardid“ (paberõpikus lk 6–11)
1. Sissejuhatus
2
- Kaart on maapinna või mõne muu pinna vähendatud, mõõtkavaline ja leppemärkidega seletatud kujutis.
- Reaalse maailma objekte ei saa ilma neid vähendamata kaardile kanda.
- Mõõtkava on matemaatiline reegel, mille järgi objekte kaardile kantakse.
Sissejuhatuseks kaartide võrdlus.
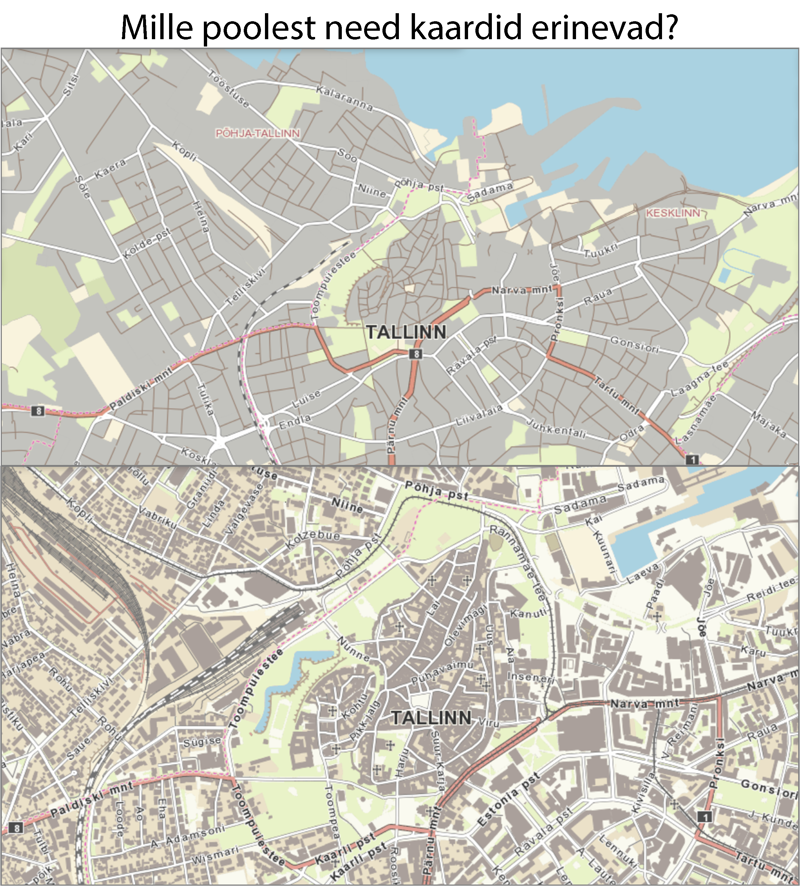
Kui tahaksime vihikusse joonistada plaani kooli ümbrusest, peaksime kõiki mõõte vähendama, et kaart paberile ära mahuks. Reaalse maailma objekte ei saa teisiti kaardile kanda, kui nende mõõtusid kaardil vähendades. Mida suuremaid piirkondi tahame kaardistada, seda vähem ruumi on kaardil iga objekti jaoks. Iga kaardi puhul on kindlaksmääratud matemaatilised reeglid, kuidas objekte kaardile kantakse. Mõõtkava ehk vähendamise aste kuulub nende reeglite hulka.
2. Mõõtkava
9
- Kaardi mõõtkava ehk vähendamise aste on suhtarv, mis näitab, mitu korda on tegelikke vahemaid kaardil vähendatud.
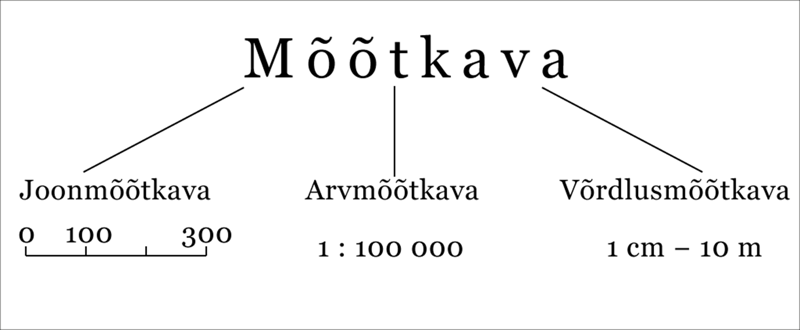
- Mõõtkava esitatakse joonmõõtkavana, arvmõõtkavana või võrdlusmõõtkavana.
- Joonmõõtkava on mõõduriba, mille jaotis näitab, kui pikad on maastikul meetrites või kilomeetrites mõõdetud jooned kaardi pinnal.
- Arvmõõtkava esitatakse suhtena, mis näitab, kui palju vastab kaardil mõõdetud ühikule samu ühikuid looduses.
- Arvmõõtkava saab esitada lihtmurruna, kus lugejas on 1 ja nimetajas arv, mis näitab, mitu korda on pikkusi vähendatud.
- Arvmõõtkava kehtib ainult konkreetse suurusega kaardi puhul. Kui kaardi suurust muuta, muutub ka mõõtkava.
- Võrdlusmõõtkava on lihtsustatud arvmõõtkava. 1 cm – 2 km tähendab, et ühele sentimeetrile kaardil vastab 2 kilomeetrit looduses.
Mõõtkava esitatakse kaartidel tavaliselt kahel viisil: joonmõõtkavana või arvmõõtkavana. Mõnikord kasutatakse ka võrdlusmõõtkava.
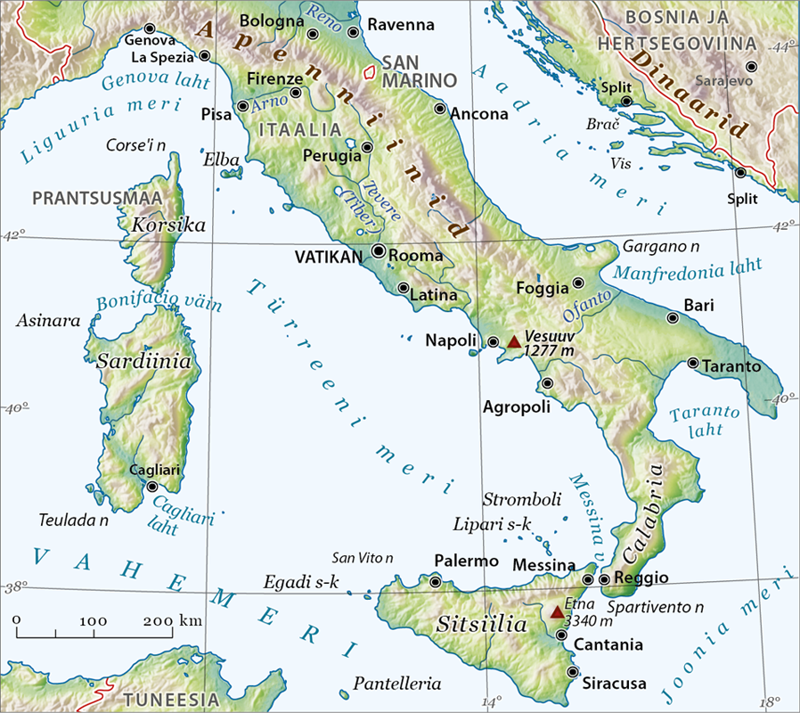
Joonmõõtkava esitab vahemaid piltlikult. See on mõõduriba, mille jaotis näitab, kui pikad on maastikul meetrites või kilomeetrites mõõdetud jooned kaardi pinnal (Itaalia kaart joonmõõtkavaga). Sirkli, pabeririba või joonlauaga on lihtne mõõta kahe punkti vahelist kaugust kaardil ja, kõrvutades seda joonmõõtkavaga, leida nende punktide tegelik vahemaa. Joonmõõtkava on eriti hea kasutada arvutikaartide puhul, sest arvutis kaarti suurendades muutub ka joonmõõtkava jaotise pikkus ja mõõtkava jääb alati õigeks.

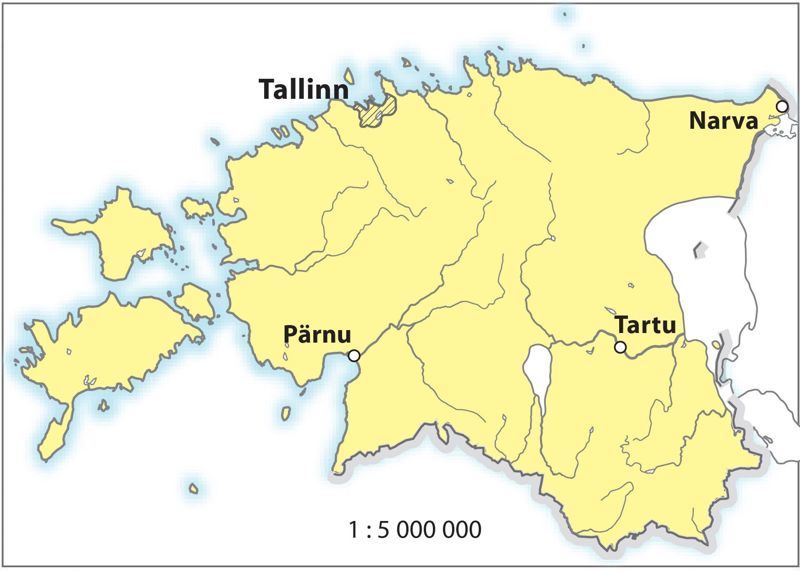
Arvmõõtkava esitatakse suhtena, mis näitab, kui palju kaardil mõõdetud ühikule vastab samu ühikuid looduses. Näiteks mõõtkava 1 : 200 000 (või ka 1/ 200 000) tähendab, et ühele sentimeetrile kaardil vastab 200 000 sentimeetrit ehk 2 kilomeetrit looduses. Arvmõõtkava on tegelikult lihtmurd, mille võib kirja panna nii, et murru lugejas on 1 ja nimetajas arv, mis näitab, mitu korda on pikkusi vähendatud. Arvmõõtkava saab kasutada ainult paberkaartidel, sest kui arvutikaartide puhul kaardi suurus muutub, ei vasta ühele sentimeetrile kaardil enam sama hulk sentimeetreid looduses, mis arvmõõtkavas kirjas on. Arvmõõtkava on määratud iga kaardi puhul konkreetse mõõduga paberi jaoks. Ka õpiku kaardid on koostatud kindlates mõõtudes, et ka raamatu trükist tulles mõõtkava täpne oleks.

Võrdlusmõõtkava on lihtsustatud arvmõõtkava. 1 cm – 2 km tähendab, et ühele sentimeetrile kaardil vastab 2 kilomeetrit looduses. Sel juhul võib kahe punkti vahemaa kaardil mõõta joonlauaga ja arvutada, kui pikk on see joon looduses. Võrdlusmõõtkava on väga lihtne kasutada, kuid samuti nagu arvmõõtkavagi, saab seda kasutada vaid paberkaartide puhul.
Ülesandeid Opiqust samal teemal
ül „Arvmõõtkava“
3. Kaartide jagamine mõõtkava alusel
3
- Kaardid jagatakse mõõtkava alusel kolme rühma: suure-, keskmise- ja väikesemõõtkavalised kaardid.
- Suuremõõtkavalistel kaartidel jääb mõõtkava vahemikku 1 : 10 000 kuni 1 : 100 000.
- Kaarte, mille mõõtkava on suurem kui 1 : 10 000, nimetatakse plaanideks.
- Keskmisemõõtkavalised kaartide mõõtkava on vahemikus 1 : 100 000 kuni 1 : 1 000 000.
- Väikesemõõtkavalised kaartide mõõtkava on väiksem kui 1 : 1 000 000.
Kaardid jaotatakse mõõtkava alusel kolme rühma: suure-, keskmise- ja väikesemõõtkavalised. Suuremõõtkavalistel kaartidel jääb mõõtkava vahemikku 1 : 10 000 – 1 : 100 000. Kuna sellisel kaardil on suur suurendus, siis mahub kaardile vaid suhteliselt väike maapinna tükk. Nendeks kaartideks võivad olla näiteks linnaplaanid, suur osa topograafilisi kaarte või ka orienteerumiskaardid. Kaarte, mille mõõtkava on suurem kui 1 : 10 000, nimetatakse plaanideks.
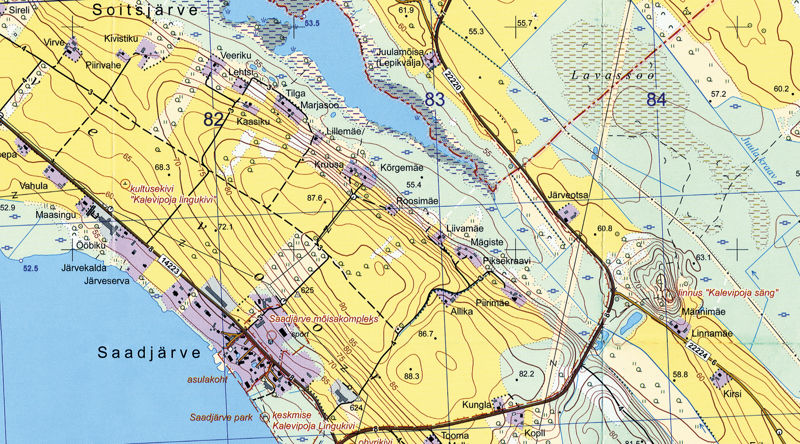
Mõõtkavaga 1 : 100 000 – 1 : 1 000 000 kaarte peetakse keskmisemõõtkavalisteks kaartideks. Neile mahuvad maakonnad ja ka väiksemad riigid. Sellised kaardid saadakse tavaliselt suuremõõtkavaliste kaartide vähendamisel ja need sobivad hästi ülevaatekaartideks.
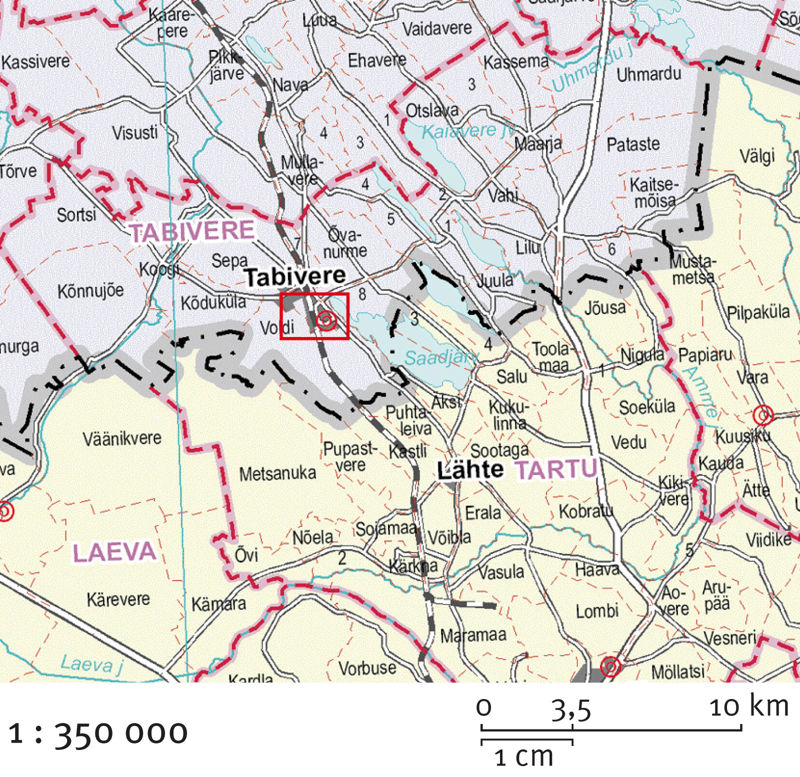
Väikesemõõtkavaliste kaartide mõõtkava on väiksem kui 1 : 1 000 000. Enamik atlasekaarte, samuti suurte riikide, madrite ja maailma seinakaardid on väikese mõõtkavaga. Väikesemõõtkavalisele kaardile mahuvad küll ulatuslikud alad, aga kõike on kujutatud lihtsustatult või isegi moonutatult.
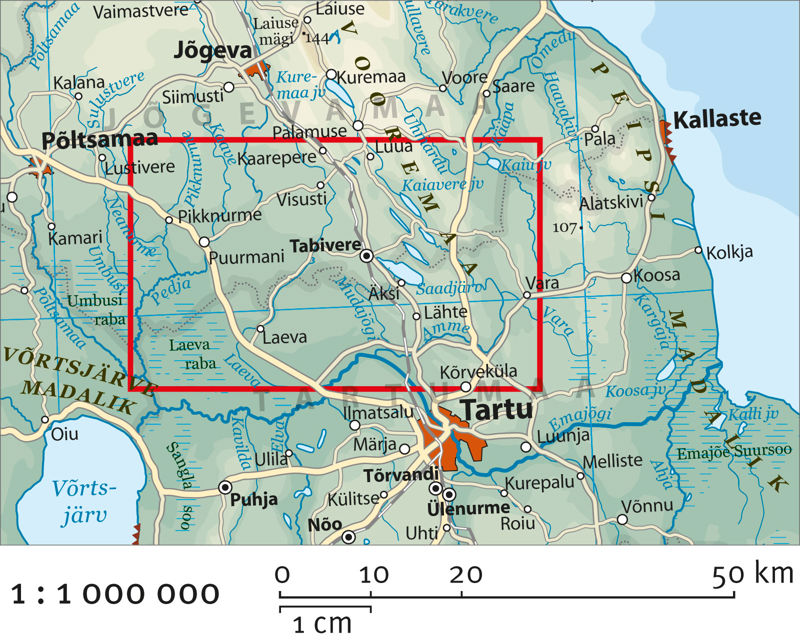
Ülesandeid Opiqust samal teemal
4. Mõõtkavade võrdlemine
15
- Mõõtkavasid saab võrrelda nagu matemaatikas murdarve.
- Mida suurem on arv murru nimetajas ehk murrujoone all, seda väiksem on mõõtkava, nt 1 : 500 > 1 : 5000
- Mida väiksem on mõõtkava, seda vähem detaile on kaardil.
- Mida väiksem on mõõtkava, seda suuremat ala kujutatakse.
Mõõtkavasid saab võrrelda samamoodi nagu matemaatikas murdarve. Mida suurem on arv murru nimetajas ehk murrujoone all, seda väiksem on mõõtkava. Näiteks 1 : 50 > 1 : 500. Mida väiksem on mõõtkava, seda vähemdetailselt on kaardil objekte kujutatud. Seega kaart mõõtkavaga 1 : 50 on oluliselt detailsem kui kaart, mille mõõtkava on 1 : 500. Mida suurem on arv murru nimetajas, seda suuremat ala kaardil kujutatakse. Aga mida suuremat ala kujutatakse, seda väiksem on mõõtkava, sest sama suurele paberile (või muule andmekandjale) peab mahtuma suurem ala. Seega saab kaardile kanda vähem infot. Sama kehtib ka vastupidi. Mida väiksem on arv murru nimetajas (või paremal pool koolonit), seda suurem on mõõtkava. Suur mõõtkava tähendab seda, et kujutatakse väiksemat ala ja selle võrra on kaart detailsem.
Samad ülesanded Opiqus
Vastused
TV ül 1


5. Vahemaade mõõtmine kaardil
9
- Kui tahame leida teekonna pikkust looduses, peame selle esmalt kaardil ära mõõtma. Seejärel saame kaardi mõõtkava järgi arvutada, kui pikk on vahemaa looduses.
- Vahemaade leidmiseks on kõige lihtsam kasutada ristkorrutist.
- Arvmõõtkava puhul arvutatakse, mitmele kilomeetrile või meetrile vastab üks sentimeeter kaardil.
Kui tahame kaardil vahemaid mõõta, peame teadma, milline on kaardi mõõtkava, olgu see väljendatud arv-, joon- või võrdlusmõõtkavana. Selleks et teada, kui suur on kahe punkti vaheline kaugus maastikul, peame esmalt mõõtma vahemaa kaardil. Seejärel saame mõõtkava järgi arvutada, kui suur on vahemaa looduses. Sellisteks arvutusteks on tavaliselt kõige lihtsam kasutada ristkorrutist. Näiteks:
Arvmõõtkava puhul arvutatakse, mitmele kilomeetrile või meetrile looduses vastab üks sentimeeter kaardil. Näiteks kui kaardi mõõtkava on 1 : 20 000, siis ühele sentimeetrile kaardil vastab 20 000 sentimeetrit looduses. Looduses on 20 000 sentimeetrit suurus, mida me hästi ette ei kujuta. See tuleks teisendada meetriteks või kilomeetriteks: 20 000 cm = 200 m = 0,2 km. Saame vastuseks, et 1 cm = 200 m. Edasi on juba lihtne vahemaid arvutada.
Samad ülesanded Opiqus
ül „Vahemaade leidmine“
Märkus: kuna ülesande lahendamine võib võtta aega, siis tasuks klassis arvutada välja esimene vahemaa ja lõpetada ülesanne kodus.
Vastused

Ülesandeid Opiqust samal teemal
ül „Tartu linna plaan“
6. Kaardi üldistamine
6
- Mõõtkavast oleneb, kui palju teavet kaardile mahub.
- Mõõtkava vähendamisega vähendatakse kaardile märgitavate objektide hulka ja detailsust.
- Kaardipildi lihtsustamist kaardi loetavuse eesmärgil nimetatakse kaardi üldistamiseks.
- Üldistades võib: vähemolulised asjad ära jätta; lihtsustada joonte kuju; liita erinevad leppemärgid üheks; nihutada leppemärke nii, et need üksteisega ei kattuks.
Mõõtkavast oleneb, kui palju teavet kaardile mahub. Suuremõõtkavalisele kaardile saab paigutada iga hoone, rändrahnu ja raja. Väikesemõõtkavalisel kaardil oleksid need aga imetillukesed ja silmale eristamatud. Seetõttu muudetakse mõõtkava vähendamisega ka kaardi välisilmet ning vähendatakse kaardile märgitavate objektide hulka ja detailsust. Et kaart oleks mõõtkava vähenedes endiselt loetav, võib
- vähemolulised asjad, näiteks väiksemad teerajad, ära jätta;
- lihtsustada joonte kuju, näiteks joonistada jõed sujuvama joonega;
- liita erinevad leppemärgid üheks, näiteks joonistada linn lihtsa ringina;
- nihutada leppemärke nii, et need üksteisega ei kattuks.
Sellist kaardipildi lihtsustamist, mille tulemusena kaardi loetavus paraneb, nimetatakse kaardi üldistamiseks. See on kartograafi ehk kaarditegija olulisim oskus – edastada vajalik kaardiinfo kasutajale selgelt ja arusaadavalt.
Samad ülesanded Opiqus
ül „Kaardi üldistamine“
7. Kokkuvõte
1
- Kaardi mõõtkava ehk vähendamise aste on suhtarv, mis näitab, mitu korda on tegelikke vahemaid kaardil vähendatud.
- Mõõtkava esitatakse joon-, arv- või võrdlusmõõtkavana.
- Kaardid jagatakse suure-, keskmise- ja väikesemõõtkavalisteks kaartideks.
- Mida väiksem on arv murru nimetajas, seda suurem mõõtkava
- Mida väiksem mõõtkava, seda enam on kaart üldistatud.
Lisamaterjal
Töölehed
- Õuesõpe. Sammu kasutamine vahemaade mõõtmisel. Staadionil või jooksurajal määratakse oma sammu pikkus ja õpitakse seda kasutama vahemaade mõõtmiseks.
- Praktiline töö. Erinevad mõõtevahendid. Õpilased mõõdavad erinevaid vahendeid kasutades esemete pikkusi ja võrdlevad tulemusi.
- Praktiline töö. Kaudsed mõõtühikud. Pikkuste mõõtmine oma keha parameetreid kasutades. Täiendavalt on võimalik teha teisendusülesandeid vanaaegsete pikkusühikutega, kasutades neid klassi või kooliümbruse mõõtmisel. Võimalus on teha vanas stiilis plaan või kaart, mis oleks vanaaegsetes pikkusühikutes
Juhendid
- Õpilaste liikumisruum. Õpilased kaardistavad nädala jooksul oma päevateekonnad ning võrdlevad neid.
Lingid ja viited
- Maa-ameti kaardirakendus X-GIS
Kodutöö ja tunni kirjeldus
Kodutöö
või

Tunni kirjeldus
Mõõtkava ja vahemaade mõõtmine (Opiqus ptk 2.4; õpikus ptk 2.4, lk 20–21) |
Teemad: kaardi mõõtkava; mõõtkava kujutamise viisid; kaartide jaotamine mõõtkavade alusel; mõõtkavade võrdlemine; vahemaade mõõtmine mõõtkavade alusel; kaardi üldistamine. |
Mõisted: mõõtkava. |
Harjutamine: TV lk 14 ül 1, 2, 3 ja lk 15 ül 6, 8. |