Arvjadad

Puuduvad arvud
Jada
Rekurrentne jada
Mõned huvitavad jadad
Kujundarvud

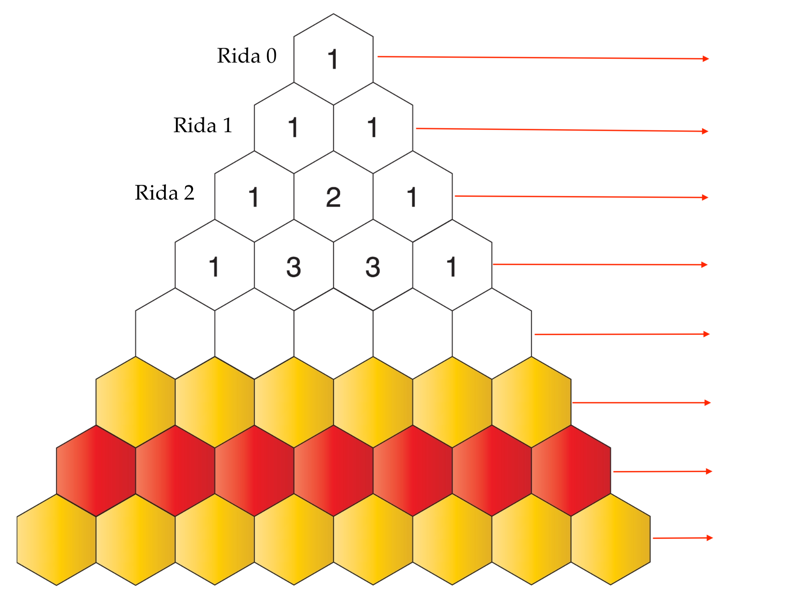
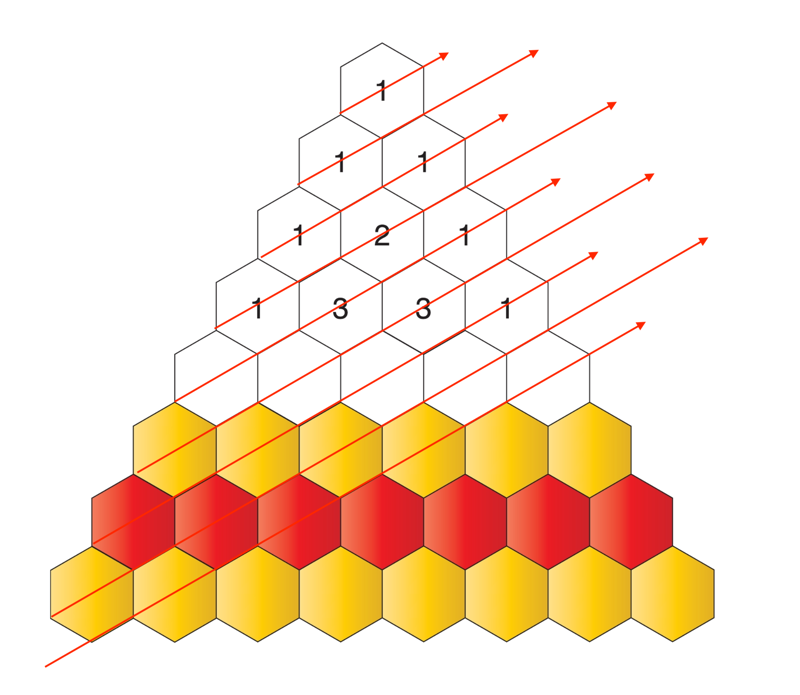
Puuduvad arvud

5; 7; 9; 11; ;
–1; 2; 5; 8; ;
7; 10; 15; 22; ;
3; 12; 27; 48; 75; ;
1; –4; 9; –16; 25; ;
2; 3; 5; 7; 11; 13; ;

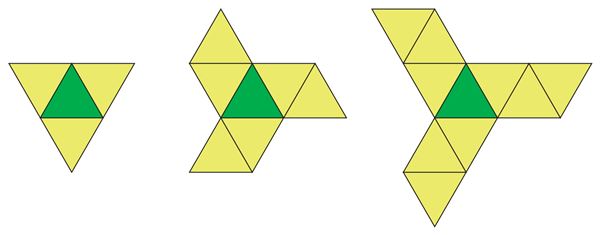
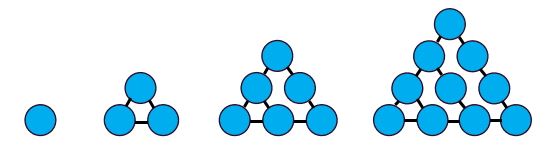
Täida tabel, kui kujundi järjekorranumber on n.

n	1	2	3	4
Kolmnurki

Leia reegel, mille järgi saab arvutada kolmnurkade arvu järjekorras n-ndal kohal olevas kujundis.

n + 3
3n + 1
2n + 3
4n – 1

Ще на цю тему

Jada

Jadaks nimetatakse järjestatud loenduvat hulka.

Järjestatud jada elemente tähistatakse
a₁; a₂; a₃; ...; a_n; ... ;
kus n ∈ ℕ on jada elemendi järjekorranumber.
Jada liiget a_n nimetatakse jada üldliikmeks.
Jada tähistatakse lühidalt selle üldliikme järgi {a_n}.

Märka

Kui on olemas valem, mis võimaldab indeksi n väärtuse järgi arvutada üldliikme a_n väärtuse, siis nimetatakse seda üldliikme valemiks.

Sel juhul

a_n = f(n).

Näited

Jada 1

Jada üldliige on $a_{n} = \frac{n + n^{2}}{2} .$

Leiame jada esimesed kolm liiget ja kümnenda liikme.

$a_{1} = \frac{1 + 1^{2}}{2} = 1$

$a_{2} = \frac{2 + 2^{2}}{2} = 3$

$a_{3} = \frac{3 + 3^{2}}{2} = 6$

$a_{10} = \frac{10 + 10^{2}}{2} = 55$

Jada üldliige on $a_{n} = \frac{{(- 1)}^{n}}{1 + 3 n} .$

$a_{1} = \frac{{(- 1)}^{1}}{1 + 3 \cdot 1} = - \frac{}{}$

$a_{2} = \frac{{(- 1)}^{2}}{1 + 3 \cdot 2} = \frac{}{}$

a₃ =

a₄ = $\frac{}{}$

Jada 3; 6; 9; 12; ... üldliikme valem on

2n² + 1
3n
4n² – 2n + 1
6n – 3

Jada 3; 9; 19; 33; ... üldliikme valem on

2n² + 1
3n
4n² – 2n + 1
6n – 3

Jada 3; 9; 15; 21; ... üldliikme valem on

2n² + 1
3n
4n² – 2n + 1
6n – 3

Ще на цю тему

Rekurrentne jada

Rekurrentseks jadaks nimetatakse jada, kus iga liige pärast esimest avaldub sellele eelnevate liikmete kaudu.

Näiteks

Tribonacci jada {T_n}.

{1; 1; 2; 4; 7; 13; 24; 44; 81; ...}

Fibonacci jada

Fibonacci jada {F_n} on rekurrentne jada

{1; 1; 2; 3; 5; 8; 13; …},

milles iga järgmine liige on kahe eelmise summa.

F₁ = F₂ = 1

F_n = F_n–₂ + F_n_–1, n ≥ 2

Luca jada

Luca jada {L_n}on rekurrentne jada

{2; 1; 3; 4; 7; 11; 18; ...},

milles iga järgmine liige alates kolmandast on kahe eelmise summa.

L₁ = 2 ja L₂ = 1

L_n = L_n_-2 + L_n_-1, n ≥ 3

Märka

Kuldlõige

Lõigu jaotamist kaheks osaks selliselt, et kogu lõigu pikkus suhtub pikema osa pikkusesse nii, nagu pikema osa pikkus suhtub lühema osa pikkusesse, nimetatakse kuldlõikeks.

$\frac{c}{b} = \frac{b}{c - b} = \frac{1 + \sqrt{5}}{2} = Φ$

Arvu Φ nimetatakse kuldlõike suhtarvuks.

Fibonacci ja kuldlõige

Fibonacci arvud on tihedalt seotud kuldlõikega. Piisavalt suure Fibonacci arvu ja sellele eelneva arvu jagatis on ligikaudu kuldlõike suhtarv.

$\frac{F_{n}}{F_{n - 1}} \approx 1,618 ... \approx Φ$

Looduses

Paljudes looduslikes protsessides või nähtustes tulevad esile Fibonacci jada liikmed. Näiteks võib neid märgata molluskite kodade ehituses.

Käbid ja õied

Fibonacci arve võib kohata karikakra õie, ananassi vilja ning käbide mustris.

Näide

Küülikute paljunemine

Oletame, et sünnib üks paar küülikuid, emane ja isane. Küülikud saavad suguküpseks ühe kuuga, paarituvad ja veel ühe kuu pärast toob emane ilmale kaks järeltulijat. Igal küülikupaaril sünnib alati üks emane ja üks isane järeltulija.

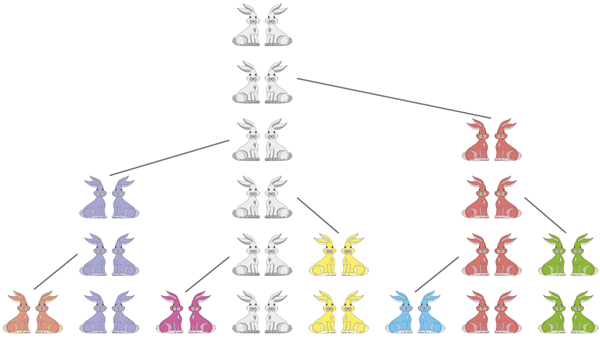
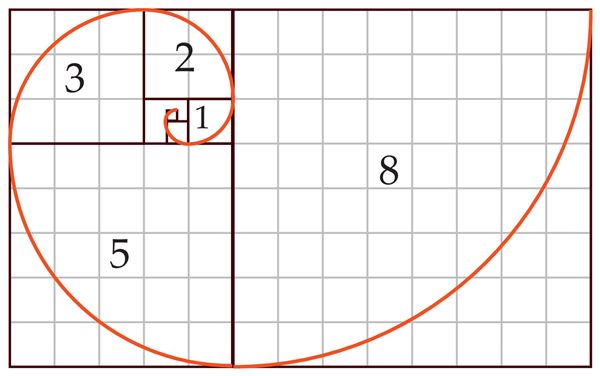
Eeldusel, et küülikud ei sure, on kolmandal kuul küülikupaare juba kaks. Kolmanda kuu lõpul toob vanima küülikupaari emane ilmale uue paari järeltulijaid. Neljandal kuul on paare seega kolm ning esimesed järeltulijad on saanud täiskasvanuks. Seega, neljanda kuu lõpus poegib juba kaks paari ja viiendaks kuuks kasvab paaride arv viieni. Kui jänesed sellise reegli järgi paljunemist jätkavad, siis on jänesepaaride hulk igal kuul võrdne Fibonacci jada vastava liikmega.

Mõtle

Millisesse arvuhulka kuulub arv Φ?

ℕ
ℝ
ℚ
ℤ
𝕀
ℂ

Lahenda ahelvõrdus

$\frac{c}{b} = \frac{b}{c - b} = Φ,$

et leida kuldlõike suhtarvu positiivne väärtus

$Φ = \frac{1 + \sqrt{5}}{2} .$

Lahendus on järgmisel slaidil.

Lahendus

Kui $\frac{c}{b} = Φ,$ siis c = bΦ.
Asendame $\frac{b}{b Φ - b} = Φ,$ millest saame ruutvõrrandi

bΦ² – bΦ – b = 0.

Jagame võrrandi liikmed b-ga.

Φ² – Φ – 1 = 0

$Φ = \frac{1 \pm \sqrt{5}}{2}$

Lahend $\frac{1 - \sqrt{5}}{2}$ on negatiivne ja $\frac{1 + \sqrt{5}}{2}$ positiivne.

Ще на цю тему

Huvitavaid jadasid

Faktoriaalide jada

a_n = n! = 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ ... ⋅ n

0! = 1

{1; 1; 2; 6; 24; 120; 720; ...}, kui n ≥ 0.

Näiteks

a₁₂= 479 001 600

Fermat’ arvude jada

Fermat’ arvudeks nimetatakse naturaalarve kujul

$F_{n} = 2^{2^{n}} + 1 .$

{3; 5; 17; 257; 65 537; 4 294 967 297; ...}, kui n ≥ 0.

Fermat’ jada viis esimest liiget on algarvud.

Alikvootjada

on naturaalarvude jada, mille iga liige alates teisest on eelneva liikme kõigi tegurite (v.a arv ise) summa.

Näiteks

Arvu 10 alikvootjada on

{10; 8; 7; 1}

Vaata-ütle jada

Jada, mille liikmete vahel pole esialgsel vaatlusel mingit seost, on oma nime vääriline.

Näiteks

Arvud 1; 11; 21; 1211; 111 221; ... on ühe vaata-ütle-jada viis esimest liiget.

Arvu 4 alikvootjada:

Arvu 8 alikvootjada:

Arvu 12 alikvootjada:

Laisa toitlustaja jada

Maksimaalse tükkide arvu jada, mis tekib, kui lõigata piiratud pinda sirgetega.

$a_{n} = \frac{n^{2} + n + 2}{2}$

Jaga pannkook võimalikult paljudeks osadeks 5 lõikega.

Vastus on järgmisel slaidil.

Kui n = 5, siis saab pannkoogi jagada maksimaalselt tükiks.

Ruudud ja kuubid

Jada üldliige a_n =

2n
n² – 2n
n²

Millisest liikmest alates ületavad jada elemendid väärtuse 2 ⋅ 10¹⁰?

Vastus

Alates liikmest n = .

Jada üldliige a_n =

3n
n³
n³ – 3n
3n²

Mitmes element tuleb korrutada 100. elemendiga, et korrutis oleks 2,7 ⋅ 10⁷?

Vastus

Element n = .

Ще на цю тему

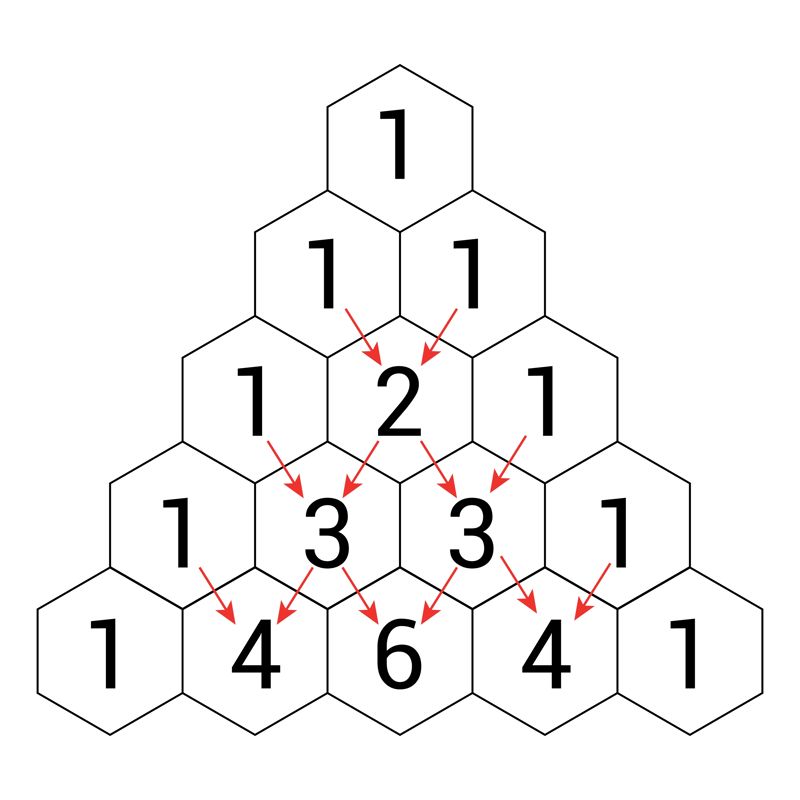
Kujundarvud

Kolmnurkarvud

Kui korrapäraseid kolmnurki konstrueerida joonisel näidatud viisil, siis punktide või ringide arvud moodustavad kolmnurkarvude jada.

K_n = {1; 3; 6; 10; 15; ...}

Ruutarvud

Kui liita kõrvutiolevad kolmnurkarvud, siis saame ruutarvude jada.

Viisnurkarvud

Viisnurkarvude jada

V_n = {1; 5; 12; 22; 35; ...}

üldliige on

$v_{n} = \frac{n (3 - n)}{2} .$

Esimesed neli viisnurkarvu

Märka

Kolmnurkarvud ei lõpe kunagi numbriga 2, 4, 7 või 9.
Iga naturaalarvu võib esitada mitte rohkem kui kolme kolmnurkarvu summana. Näiteks 51 = 15 + 36.

Leia iga ruutarvu erinevus naaberarvust ja reasta tulemused. Saadud jada üldliige on

2n – 1
3n – 2
2n + 1
4n – 3

Leia iga kolmnurkarvu erinevus naaberarvust ja reasta tulemused. Saadud jada üldliige on

n + 1
2n
2n –1
3n – 2

Leia iga viisnurkarvu erinevus naaberarvust ja reasta tulemused. Saadud jada üldliige on

3n –1
3n + 1
4n – 1
4n + 1

Näide

Hulknurkarvude jadad

Kuusnurkarvude jada üldliige

$h_{n} = \frac{4 n^{2} - 2 n}{2} = 2 n^{2} - n$

Seitsenurkarvude jada üldliige

$h_{n} = \frac{5 n^{2} - 3 n}{2}$

Tuhatnurkarvude jada üldliige

$h_{n} = \frac{9998 n^{2} - 9996 n}{2}$

Ще на цю тему

Harjuta ja treeni

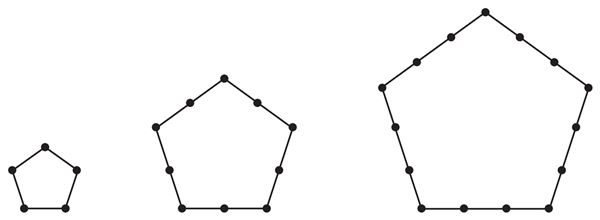
Selle jada viisnurkade külgedel olevate täppide arvu üldliige
a_n =
Kahekümnendal viisnurgal on
a₂₀= täppi.

Tõesta

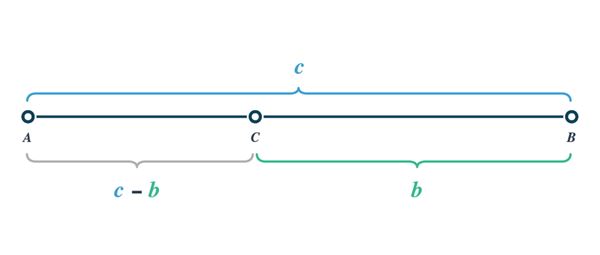
Kuldlõike suhtarvul on üks huvitav omadus: tema pöördväärtus on täpselt ühe võrra väiksem kui arv ise.

$\frac{1}{Φ} = Φ - 1$

Tõesta see omadus kuldlõike definitsiooni põhjal:

$\frac{c}{b} = \frac{b}{c - b} = \frac{1 + \sqrt{5}}{2} = Φ$ .

Jada liikmed on 13 ; 14 ; 15 ; 16;...
- Üldliige $a_{n} = \frac{}{}$
- a₁₈ =
Jada liikmed on 5,5; 8; 10,5; 13; 15,5; ...
- Üldliige a_n =
- a₁₁ =

Sellise püramiidi põhjakihis olevate kuupide arvu üldliige a_n =

4n
4n – 3
4n – 4
n²
4n²
4n² – 4

Kui püramiidis oleks kihte 17, siis kõige alumises kihis oleks kuupi.

3;; 11 13; 3113
2; 12; ;
; 312 211;

Ще на цю тему

Ekstra

Pascali kolmnurk

Pascali kolmnurk on lõpmatu kolmnurkne tabel, mille iga element on eelmises reas tema kohal paiknevate elementide summa.
Iga rea esimene ja viimane arv on 1.

Printimiseks

Pascali kolmnurga read 0 kuni 4. Kõige ülemine arv 1 on rida järjekorranumbriga 0.

Vihje

Pascali kolmnurga tipus on arv 1 ja selle rea järjekorranumber on null.
Reas nr 1 ehk esimeses reas on arvud 1 ja 1.

Arvudega 1 ja 11 algab rida.
Arv 36 asub 3. kohal reas.
Reas nr 12 on arvu.
11.reas on viiega jaguvat arvu.
7. reas olevate arvude summa on

Jadad Pascali kolmnurgas

Pascali kolmnurga igas reas asuvad elemendid järjekorranumbriga 0, 1, 2, 3, ... n.

2^–1
2⁰
2¹
2²
2³
3²
2⁴
2⁵
5²
2⁶
2⁷

Reas nr 21 asuvate arvude summa algarvu astmena on .

Järeldus

Ridade summad moodustavad arvu astmete jada, kus rea number on

võrdne astendajaga.
astendajast 1 võrra suurem.
astendajast 1 võrra väiksem.

Elemendid nr 0 asuvad esimesel diagonaalil ja moodustavad

täisarvude jada
naturaalarvude jada
paarisarvude jada
konstantse jada

Elemendid nr 1 asuvad teisel diagonaalil ja moodustavad

täisarvude jada
naturaalarvude jada
paarisarvude jada
konstantse jada

Elemendid nr 2 asuvad diagonaalil ja moodustavad jada, , , , , ... See on Jada liga liige avaldub valemiga A_n=

$\frac{n (n + 1)}{2}$
$\frac{n (n + 1)}{3}$
$\frac{n (n + 1) (n + 2)}{6}$
$\frac{n (n + 1) (n + 2) (n + 3)}{24}$

Neljandal diagonaalil on jada
1, , , , , ... .
Seda nimetatakse tetraeederarvude jadaks. Jada iga liige avaldub valemiga T_n=

$\frac{n (n + 1)}{2}$
$\frac{n (n + 1)}{3}$
$\frac{n (n + 1) (n + 2)}{6}$
$\frac{n (n + 1) (n + 2) (n + 3)}{24}$

Liida arvud, mis asuvad laugetel diagonaalidel.

Järgmisel laugel diagonaalil olevate arvude summa on .
Need summad moodustavad

Fibonacci jada.
Fermat' arvude jada.
allikvootjada.

Arvu 11 astmete jada

Pane tähele, et Pascali kolmnurga esimestes ridades moodustavad numbrid arvu 11 astme. Otsime ka teistest ridadest vastavat arvu 11 astet.

reas on üks üks, 1=11^0.
reas on kaks ühte, 11=11^1.

Uurime, kas ka järgnevates ridades on arvu 11 vastav aste.

Rida	11^n=vastus	Numbrid reas
2.	=	121
3.	=	1331
4.	=	14641
5.	11^5=

Kui Pascali kolmnurga reas on ühekohalised arvud, on 11 astmeid lihtne näha. Alates 5.reast tuleb arvu 11 astme leidmiseks appi võtta kümnendsüsteemi arvu järgud.

Näidaku Pascali kolmnurga iga rea viimane arv üheliste arvu, eelviimane kümneliste arvu, sellele eelnev sajaliste arvu jne. Seda reeglit järgides moodustame alates 5.reast kümnendsüsteemi arvud.

reas on ühelisi 1, kümnelisi 5, sajalisi 10, tuhandelisi 10, kümnetuhandelisi 5 ja sajatuhandelisi 1.

1+5\cdot10+10\cdot10^2+10\cdot10^3+5\cdot10^4+1\cdot10^5=
=11^5

reas on

1+\cdot10+\cdot10^2+20\cdot10^3+15\cdot+\cdot+1\cdot10^6==11^6

reas on

=11^7

Jätka vihikus arvu 11 astmete leidmist.

Ще на цю тему

Послугу здійснює Star Cloud OÜ

Приєднайтесь до Opiq

Прогрес в Opiq

	Роботи
	Параграф опрацьовано

Arvjadad

Ще на цю тему

Puuduvad arvud

Ще на цю тему

Jada

Jada

Märka

Näited

Jada 1

Ще на цю тему

Rekurrentne jada

Rekurrentne jada

Näiteks

Fibonacci jada

Luca jada

Märka

Kuldlõige

Fibonacci ja kuldlõige

Looduses

Käbid ja õied

Näide

Küülikute paljunemine

Mõtle

Lahendus on järgmisel slaidil.

Lahendus

Ще на цю тему

Huvitavaid jadasid

Faktoriaalide jada

Näiteks

Fermat’ arvude jada

Alikvootjada

Näiteks

Vaata-ütle jada

Näiteks

Laisa toitlustaja jada

Vastus on järgmisel slaidil.

Ruudud ja kuubid

Vastus

Vastus

Ще на цю тему

Kujundarvud

Kolmnurkarvud

Ruutarvud

Viisnurkarvud

Märka

Näide

Hulknurkarvude jadad

Ще на цю тему

Harjuta ja treeni

Tõesta

Ще на цю тему

Ekstra

Pascali kolmnurk

Vihje

Jadad Pascali kolmnurgas

Järeldus

Arvu 11 astmete jada

Ще на цю тему

Додати матеріал

Файли для завантаження

Повідомити про помилку

Сюди пишіть лише про помилки Opiq. Будь ласка, опишіть помилку якомога детальніше.

Якщо Ви погоджуєтеся поділитися інформацією про себе, повідомте свої контактні дані (e-mail, телефон).

Поставте галочку, щоб допомогти нам боротися зі спамом

Opiq використовує файли cookie