Ringjoon. Ringjoone pikkus

Mis on ringjoone diameeter?
Kuidas arvutada ringjoone pikkust?

Seotud sisu

Ringjoone raadius ja diameeter

Sirkli ajalugu

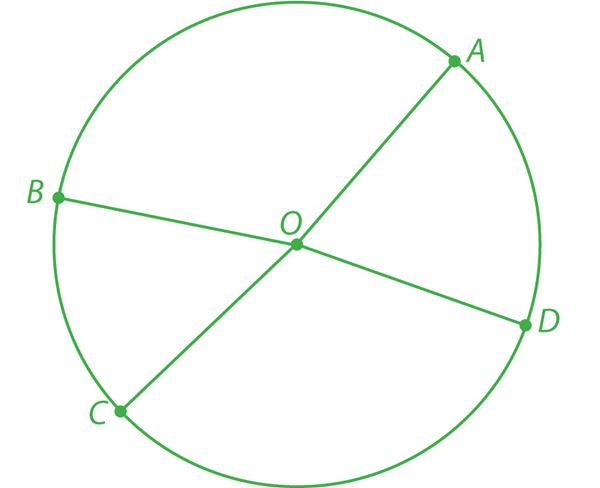
OA = mm

OB = mm

OC = mm

OD = mm

Kuna lõik sirkli haarade otspunktide vahel oli kogu aeg sama, siis kinnitas ka mõõtmine, et kõik ringjoone punktid asuvad punktist O võrdsel kaugusel. Seda punkti nimetatakse ringjoone keskpunktiks[mõiste: ringjoone keskpunkt – punkt, millest ringjoone kõik punktid asetsevad ühel ja samal kaugusel].

Ringjoone kõik punktid asetsevad ringjoone keskpunktist ühel ja samal kaugusel.

Ringjoone keskpunkti ringjoone mis tahes punktiga ühendavat lõiku ja ka selle lõigu pikkust nimetatakse ringjoone raadiuseks[mõiste: ringjoone raadius – lõik, mis ühendab ringjoone keskpunkti ringjoone mis tahes punktiga].

Raadiust tähistatakse
tähega r.

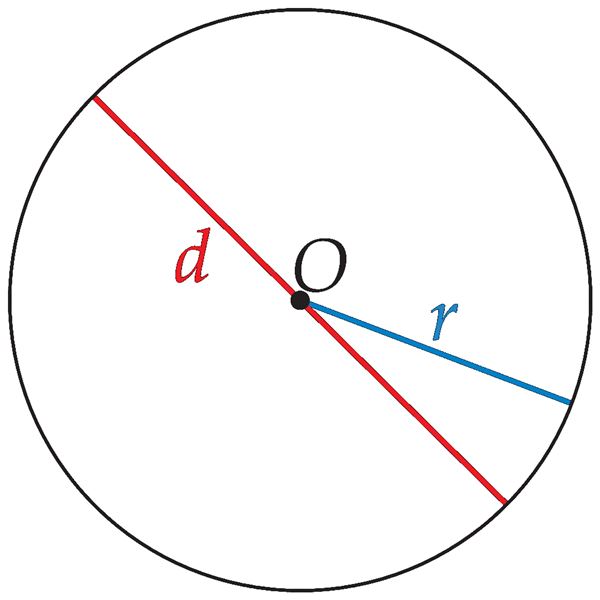
Lõiku, mis läbib ringjoone keskpunkti ja ühendab ringjoone kahte punkti, nimetatakse ringjoone diameetriks[mõiste: ringjoone diameeter – lõik, mis läbib ringjoone keskpunkti ja ühendab ringjoone kahte punkti].

Diameetrit tähistatakse tähega d ning see on raadiusest kaks korda pikem, seega d = 2r.

Raadius	2,5 cm	0,4 dm	cm	dm
Diameeter	cm	dm	10,8 cm	0,5 dm

Seotud sisu

Ringjoone pikkus

Kuidas leida ringjoone pikkust

Juba kauges minevikus märkasid teadlased, et mis tahes ringjoon on kindel arv kordi pikem selle diameetrist. See arv tähistati kreeka väiketähega π[mõiste: arv π – arv, mis saadakse ringjoone pikkuse ja ringjoone diameetri jagamisel ja mille ligikaudne väärtus on 3,14] (loe: pii).
Ringjoone pikkust tähistatakse tähega C.

$\frac{ringjoone pikkus}{ringjoone diameeter} = π$ ehk $\frac{C}{d} = π$

Siit saame ringjoone pikkuse valemi.

C = πd

Ringjoone pikkus on diameetrist π korda suurem.

Kuna ringjoone diameeter on raadiusest kaks korda pikem, st d = 2r, võime kirjutada ka nii:

C = 2πr

Vana-Kreeka teadlane Archimedes (287.–212. a eKr) tegi kindlaks, et π väärtus on arvude $3 \frac{10}{71}$ ja $3 \frac{1}{7}$ vahel.

Arv π on lõpmatu mitteperioodiline kümnendmurd, mille mõned esimesed kohad on järgmised:
π = 3,14159265358979...

Huvitav teada

14. märts on rahvusvaheline π‑päev (kolmanda kuu ehk märtsikuu
14. päev).

Esimest korda tähistati seda päeva 1988. aastal San Francisco teaduspargis, kus kohal olnud liikusid ringides ja sõid õunakooki. Põhjus selles, et inglise keeles häälduvad π ja pie (kook) sarnaselt.

Matemaatikahuvilised võistlevad sel päeval π komakohtade meeldejätmises, praegune rekord on üle 67 000 komakoha. See kuulub hiinlasele, Lu Chaole. Pii 67 890 komajärgse koha eksimatu ettelugemine võttis tal aega 24 tundi ja neli minutit.

Ülesannete lahendamisel kasuta π ligikaudset väärtust.

π ≈ 3,14 või π ≈ $\frac{22}{7}$

Näide

Arvutame ringjoone pikkuse, kui diameeter on 7 cm.

C = πd

C ≈ 3,14 · 7 ≈ 21,98 (cm)

või

C ≈ $\frac{22}{7}$ · 7 ≈ 22 (cm)

Seotud sisu

Katsetan ja uurin

Kasutage silindrikujulisi kehi: kruusi, teeklaasi vms. Kirjutage mõõdud tabelisse.

Arvutage iga mõõdetud ringjoone pikkuse ja diameetri jagatis (tulemus ümardage sajandikeni).

Ringjoone pikkus C
Diameeter d
C : d

Võrrelge saadud jagatisi π väärtusega. Mida märkate?

Soovitus. Täpsema ümbermõõdu saamiseks kerige niiti (traati) mitu keerdu tihedalt üksteise kõrvale ja jagage saadud pikkus keerdude arvuga.

Seotud sisu

Matemaatikaklubi

Kaspar ja Ott seisavad ringikujulise jooksuraja ühe diameetri erinevates otspunktides. Mõlemad alustavad samal ajal päripäeva jooksmist, kusjuures Oti kiirus on $\frac{9}{8}$ Kaspari kiirusest.