Punkti koordinaadid ruumis

Koordinaatteljed
Punkti kirjeldamine koordinaatide abil
Kahe punkti vaheline kaugus

Punkt ruumis

Kui tahame määrata punkti koordinaate kolmemõõtmelises ruumis, peame lisama kahele olemasolevale teljele veel kolmanda. Seda telge nimetatakse aplikaatteljeks ehk z-teljeks.

Punkti P z-koordinaadiks on selle ristprojektsioon z₁ z-teljel.

Seega saame koordinaadid

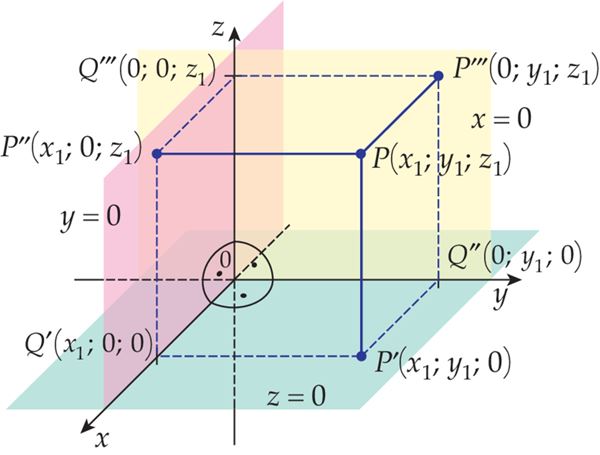
P(x₁; y₁; z₁) ja P´(x₁; y₁; 0), kui projekteerime punkti xy-tasandile.

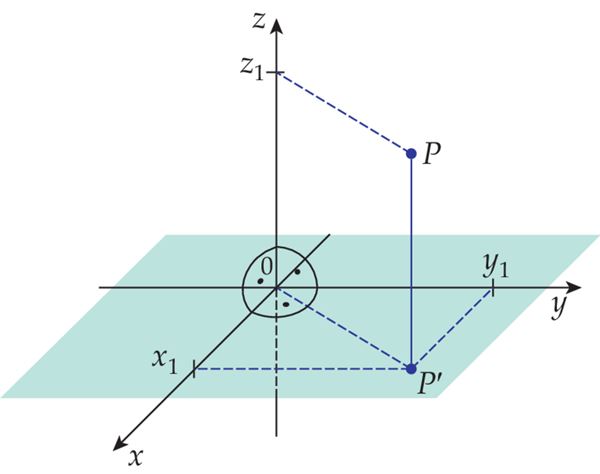
Punkti asukoha kirjeldamine ruumis
P(x₁, y₁, z₁)

Märka

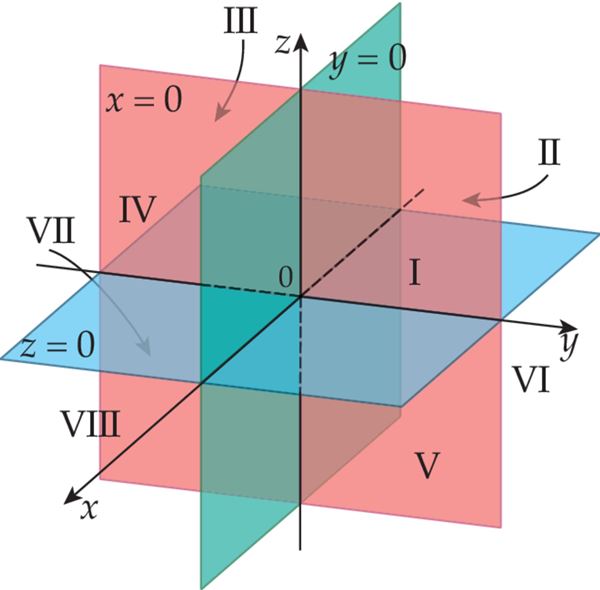
Tasandeid, millel asuvad kaks koordinaattelge kolmest, nimetatakse koordinaattasanditeks. Need on xy-tasand, xz-tasand ja yz-tasand.

Kui punkti z-koordinaat on null, siis asub see punkt xy-tasandil, P(x₁; y₁; 0).
Kui punkti y-koordinaat on null, siis asub see punkt xz-tasandil, P(x₁; 0; z₁).
Kui punkti x-koordinaat on null, siis asub see punkt yz-tasandil, P(0; y₁; z₁).

Kui tahame leida punkti projektsioone telgedel, peame võrdsustama kaks koordinaati nulliga. Punkti P(x₁; y₁; z₁) projektsioon x-teljel on Q′(x₁; 0; 0), projektsioon y-teljel on Q″(0; y₁; 0) ja projektsioon z-teljel Q‴(0; 0; z₁).

P(2; 3; 0) asub
P(–1; 0; 3) asub
P(0; –3; –2) asub
P(2; 0; 0) asub
P(0; –1; 0) asub
P(0; 0; 5) asub

Näide 1

Punkti asukoha kirjeldamine ruumis P(x₁, y₁, z₁)

Koordinaattasandid jaotavad ruumi kaheksaks oktandiks

Seotud sisu

Punktide vaheline kaugus

Vaatleme kahte punkti
P(x₁; y₁; z₁) ja Q(x₂; y₂; z₂).

Leiame nendevahelise kauguse.

Projekteerime mõlemad punktid xy-tasandile,
saame punktid:
P′(x₁; y₁; 0), Q′(x₂; y₂; 0).

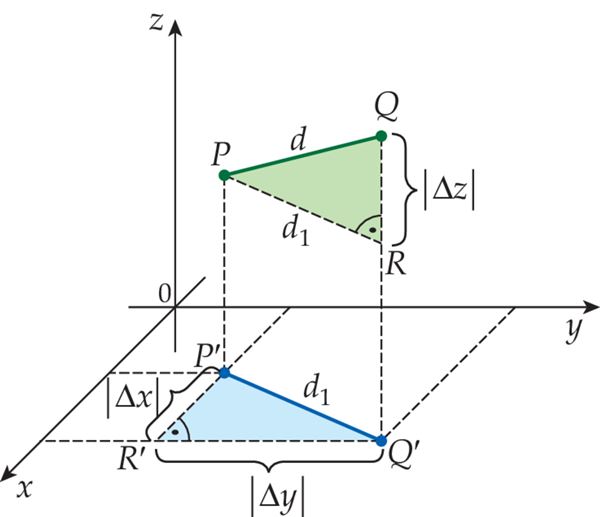
Nende punktide vaheline kaugus d₁ järeldub Pythagorase teoreemist (Δx ja Δy on koordinaatide muudud).

$d_{1} = \sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}} =$
$= \sqrt{{(∆ x)}^{2} + {(∆ y)}^{2}}$

Tasandil, millel asuvad punktid P, Q, P′ ja Q', on täisnurkne kolmnurk PQR, mille kaatetiteks on d₁ ja $|∆ z| = |z_{1} - z_{2}|$ ning hüpotenuusiks otsitav kaugus d, mille leiame Pythagorase teoreemi järgi.

$d = \sqrt{{d_{1}}^{2} + {(∆ z)}^{2}} =$ $\sqrt{{(∆ x)}^{2} + {(∆ y)}^{2} + {(∆ z)}^{2}}$
ehk
$d = \sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2} + {(z_{1} - z_{2})}^{2}}$

Kahe punkti, P(x_1;y_1;z₁) ja Q(x₂_; y₂_; z₂), vaheline kaugus d.

$d = \sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2} + {(z_{1} - z_{2})}^{2}}$

Punktide projektsioonid on järgmised:

A′(–3; –1; 0), B′(1; –4; 0);
A″(–3; 0; 4), B″(1; 0; –8);
A‴(0; –1; 4), B‴(0; –4; –8).

Punktidevaheline kaugus on ruutjuur vastavate koordinaatide muutude ruutude summast.

$d = \sqrt{^{2} +^{2} +^{2}} =$
$= \sqrt{169} = 13$

A(2; 0; 0), B(5; 0; 0),
seega d_AB = .
M(2; 1; 0), N(5; –1; 0),
seega d_MN ≈ .
S(2; 1; –4), T(5; –1; 1),
seega d_ST ≈ .
O(0; 0; 0), K(–1; –1; –1),
seega d_MN ≈ .
O(0; 0; 0), L(2; 2; z), d_OL = $2 \sqrt{3}$ ,
seega z₁ = < z₂ = .
U(0; 1; z), H(1; 1; 1), d_UV = $\sqrt{2}$ ,
seega z₁ = < z₂ = .

Seotud sisu

Harjuta ja treeni

(0; 0; 0)
(2; 0; 0)
(0, 2; 0)
(0; 0; 2)
(2; 3; 0)
(3; 2; 0)
(0; 3; 0)
(0; 3; 2)
(0; 3; 4)
(3; 4; 0)
(0; 0; 4)
(2; 0; 4)
(2; 4; 0)
(2; 3; 4)
(3; 2; 4)
(4; 2; 3)
(2; 4; 3)

$\sqrt{13}$
$\sqrt{29}$
$\sqrt{20}$
2
3
4
5

AC =	HG =
BD =	DF =
BG =	AG =

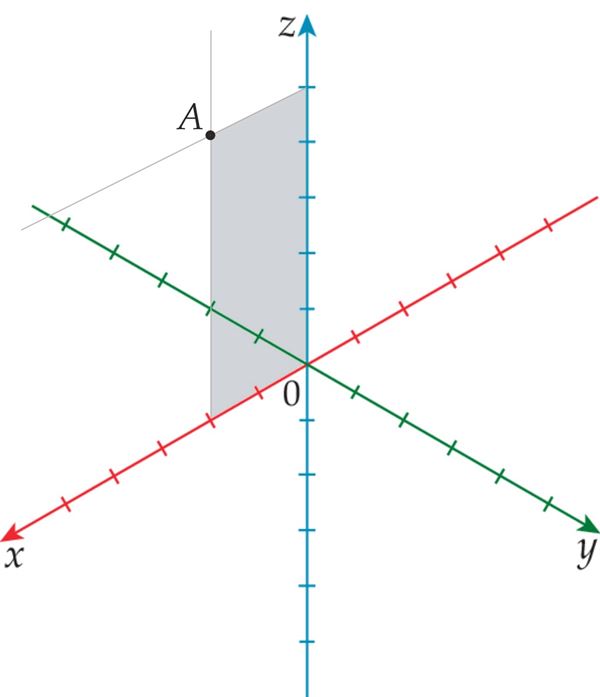
z-teljel punkt

B(0; 0; 5);
B(0; 0; 2⁵)
B(5; 0; 5)
B(–120; 0; 5)
B(2²⁰; 0; 5 )
B(2^–15; 0; 5)

xy-tasandil võrdne lõigu pikkusega

B(0; 0; 5)
B(2; 4, 5)
B(12; –15; 0)
B(–10; –1; 5)
B((–2)⁷; 8; 5)
B(90; 68; –5)

3) yz-tasandil võrdne lõigu pikkusega

B(2; 0; 0)
B(2; 4, 5)
B(2; –1; 0)
B(–10; 2; 5)
B(2; 2¹⁰; 100)
B(9; –6; 2)

A(–2; –5; 3) ja
B(3; 1; 4)?
Vastus. h = $\sqrt{}$
A(–2; –5; 3) ja
B(2; –3; 2)?
Vastus. h = $\sqrt{}$

A(–2; –5; 3) ja B(3; 1; 4)

Seotud sisu

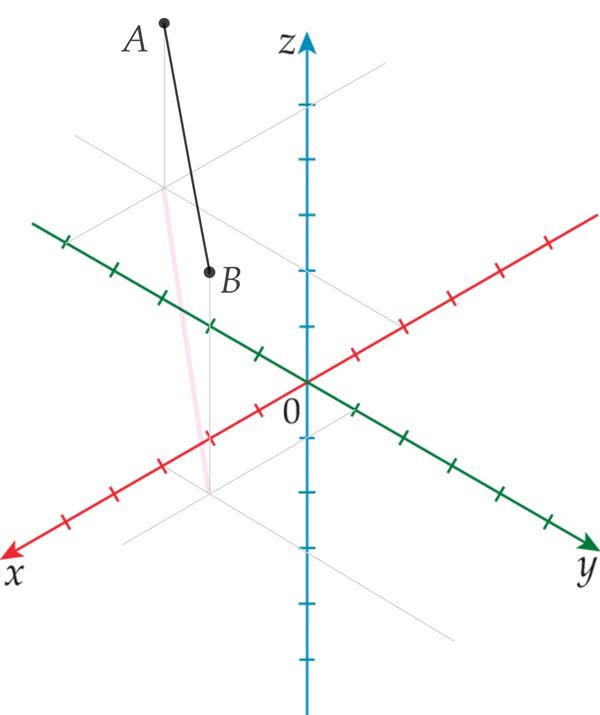
Punkt tasandil, punkt ruumis

P(2; –3)
$\sqrt{(1 - 2)^{2} + (1 - (- 3))^{2}}$
P(1; 2; –3 )
$\sqrt{(1 - 1)^{2} + (1 - 2)^{2} + (1 - (- 3))^{2}}$

Punkt tasandil

Punkt ruumis

Punkti P ja Q(1; 1) vaheline kaugus tasandil

Punkti P ja Q(1; 1; 1) vaheline kaugus ruumis

P(x; y; z) asub x-teljel, siis

x = 0
y = 0
z = 0

P(x; y; z) asub y-teljel, siis

x = 0
y = 0
z = 0

P(x; y; z) asub z-teljel, siis

x = 0
y = 0
z = 0

P(x; y; z) asub xy-tasandil, siis

x = 0
y = 0
z = 0

P(x; y; z) asub yz-tasandil, siis

x = 0
y = 0
z = 0

P(x; y; z) asub xz-tasandil, siis

x = 0
y = 0
z = 0

Seotud sisu

Teenust osutab Star Cloud OÜ

Liitu Opiquga

Opiqus edenemine

	Tööd
	Peatükk on läbi töötatud

Punkti koordinaadid ruumis

Seotud sisu

Punkt ruumis

Märka

Näide 1

Seotud sisu

Punktide vaheline kaugus

Seotud sisu

Harjuta ja treeni

Seotud sisu

Punkt tasandil, punkt ruumis

Seotud sisu

Lisa materjali

Lisatavad failid

Teata veast

Teata siia ainult Opiqu veast. Palun kirjelda viga nii täpselt kui võimalik.

Kui ootad Opiqu meeskonnalt vastust, lisa oma kontaktandmed (e-post, telefon).

Tee linnuke, et aidata meil spämmiga võidelda

Opiq kasutab küpsiseid