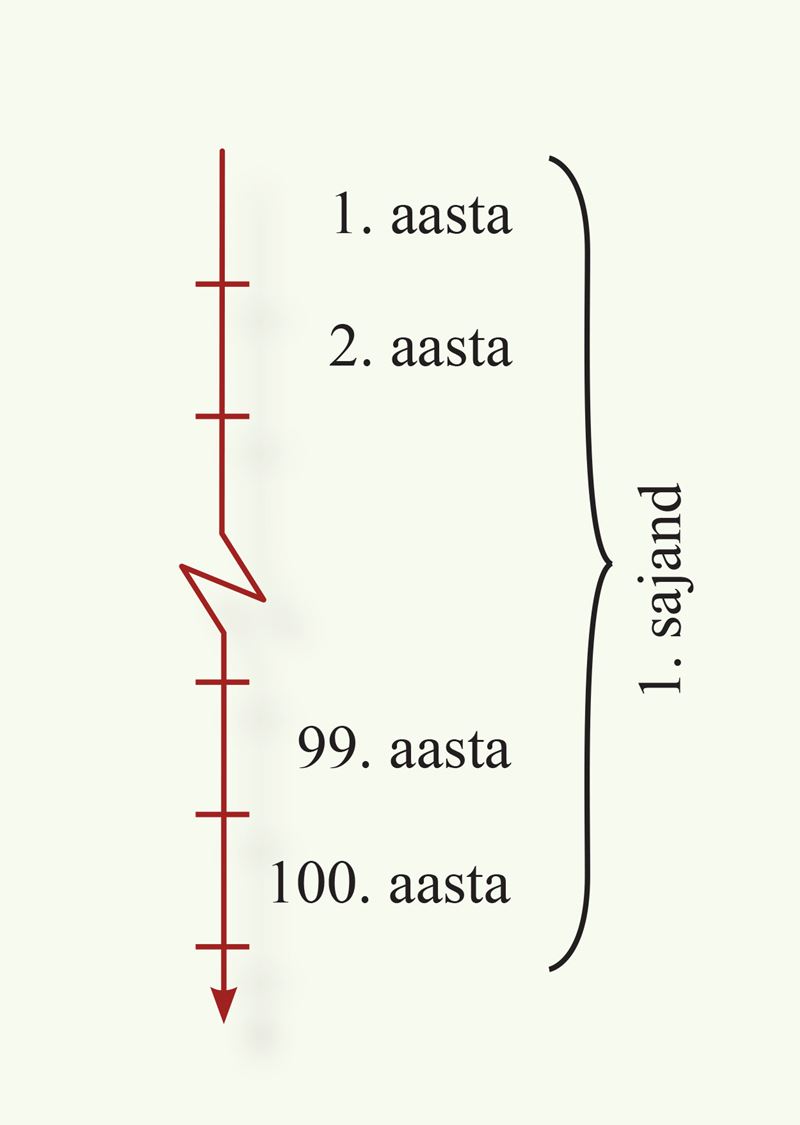
- Mitmendal sajandil ja mitmendal aastatuhandel (millenniumil) õpik ilmus?
Vastus. See õpik ilmus sajandil ja aastatuhandel. - Millal algasid eelmise küsimuse vastuses nimetatud sajand ja aastatuhat?
Vastus. Nimetatud sajand ja aastatuhat algasid aastal . - Millal algab pärast selle õpiku ilmumist uus sajand ja millal uus aastatuhat?
Vastus. Uus sajand algab aastal ja uus aastatuhat algab aastal . - Mitu aastat, kuud ja päeva on möödunud käesoleva sajandi algusest sel päeval, kui Sa lahendad seda ülesannet?
Vastus. Täna on möödunud käesoleva sajandi algusest aastat, kuud ja päeva.
 | ||||||

Vastus. Rukki perel tuleb novembris maksta kogu pere leiva eest € võrra rohkem kui oktoobris.
Vastus. Piima hind tõusis % võrra. Piima eest saadud sissetulek muutus % võrra.
- Kui palju maksab Artur tegelikult telefoni eest, kui ta ostab selle järelmaksuga? Kui mitme protsendi võrra on telefon järelmaksuga ostes kallim?
Vastus. Artur maksab järelmaksuga ostes telefoni eest eurot.
Järelmaksuga ostes on telefon % võrra kallim. - Tee vastavad arvutused ka Martini ostusoovi kohta.
Vastus. Martin maksab järelmaksuga ostes telefoni eest eurot.
Järelmaksuga ostes on telefon % võrra kallim. - Võrdle Arturi ja Martini ostusoove.

Vastus. Sääsetõrjevahendis on ‰ toimeainet.
Vastus. Peetril oli % võrra rohkem pooldajaid kui Ukul. Küsitluslehe jättis täitmata õpilast.
Üksliikmed
- 2 · 3 · 5 · 22 · 4
- a · b3 · m · 52 · 2
- (–2)3 · x5 + u · v
- 2a – 4 + 5n · 7
- 4 · 52 · u2 · m · 2x
- k · 5 · 4 · 2 · a · b2
Üksliikmed kirjuta normaalkujul vihikusse.
Näide. 2 · a3 · 5 · x · x · x · x · m2 = 10a3m2x4
5a3 =
5x2y5 =
–5m4np2 =
=
mn6p =
Võrrandid
Vastus. Need arvud on ja .
- Lahenda võrrand.
5(x + 5) – 24 = 13(2x – 3) – 10,4
x = - Suurenda saadud lahendit 25% võrra.
Vastus. Saadud arv on. - Aseta leitud arv avaldisse muutuja a asemele ja arvuta selle avaldise väärtus.
Vastus. Selle avaldise väärtus on. - Leia saadud arvust ja seejärel uue arvu vastandarv.
Vastus. Uue arvu vastandarv on. - Näita, et viimati leitud arv on võrrandi lahend.
Lineaarfunktsioon

Esita vihikus graafiliselt nende kinganumbrite vaheline seos, märkides rõhtteljel Eesti kinganumbrid.
Kas seos on võrdeline? Aga lineaarne?
Vastus. See seos on .
Muutujate x ja y väärtuste paar | (0; 2) | (0; –2) | (6; –4) |
Vabaliikme b väärtus |
 | ||||||
- Leia valemi kujul üldine seos, mis võimaldab Celsiuse skaala näidu järgi arvutada temperatuuri Fahrenheiti kraadides.
°F =°C + - Milline on Sinu keha normaalne temperatuur Fahrenheiti skaala järgi?
Vastus. See on °F. - Missuguse temperatuuri juures Fahrenheiti järgi vesi keeb?
Vastus. °F juures. - Missugusel temperatuuril on termomeetri näit Celsiuse ja Fahrenheiti skaalal arvuliselt võrdne?
Vastus.°C = °F
Kujundid
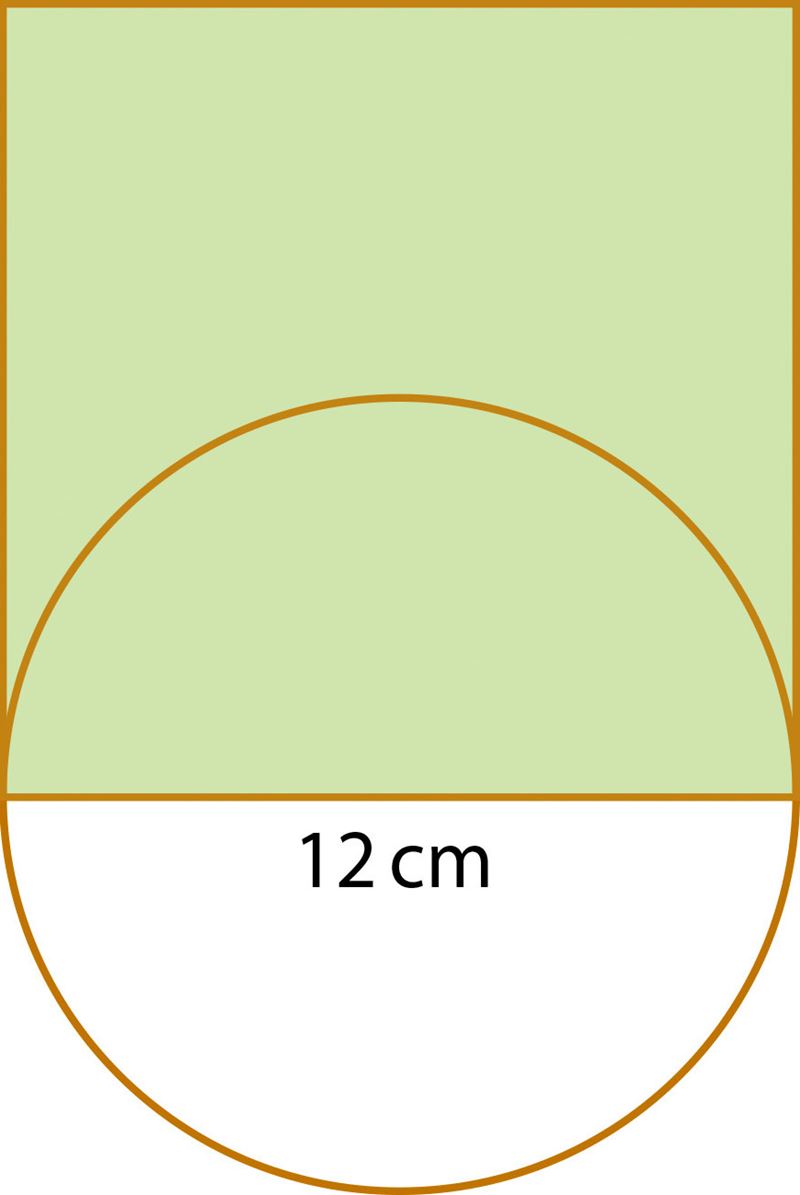
- ruudu pindalast kuulub ringile?
Vastus. Ligikaudu %. - moodustab ringi ümbermõõt ruudu ümbermõõdust?
Vastus. Ligikaudu %.
- on ringi ümbermõõt ruudu ümbermõõdust väiksem?
Vastus. Ligikaudu %. - on ruudu ümbermõõt ringi ümbermõõdust suurem?
Vastus. Ligikaudu %.
Uuri, kas arvutustulemus oleneb ruudu külje pikkusest.
Vastus. Ruudu pindala moodustab ringi pindalast ligikaudu %.
Vastus. Kasti ruumala korda ehk % võrra.
Uuri, kas arvutuse tulemus oleneb kasti mõõtmetest ja nende järjestusest.
Vastus. S = cm2.
Vastus. Kolmnurga nurgad on °, °, °.
Vastus. Alus on cm ja haar cm.
Vastus. Rööpküliku lähisnurgad on ° ja °.
Vastus. S = cm2.
Arvu standardkuju
Näide.
= =
Standardkujulise arvu esimene tegur on teisendatud ühekohalise täisosaga arvuks. Selleks tuleb eelmise korrutise esimest tegurit 59 vähendada koma tõstmisega 10 korda. Et võrdus kehtima jääks, tuleb teist tegurit suurendada 10 korda, liites kümne astendajale ühe.
Kirjuta standardkujul, kui kaugel Päikesest liiguvad keskmiselt selle kolm lähimat planeeti.
- Merkuur – 57 900 000 km = km
- Veenus – 108 000 000 km = km
- Maa – 150 000 000 km = km
Näide 1.
Pane tähele: kui 10 astendaja on negatiivne täisarv, siis selle astme esituses kümnendmurruna on nullide arv võrdne astendaja absoluutväärtusega.
Näide 2.
Kirjutame arvu 0,000 000 0275 standardkujul. Siis saame:
.
Pane tähele: ühest väiksema arvu esitamiseks standardkujul on saadud korrutises esimene tegur teisendatud ühekohalise täisosaga arvuks koma liigutamisega paremale. Kümne astendaja vastandarv näitab, mitme koha võrra on sealjuures koma liigutatud.
Kirjuta arv standardkujul.
- Maakoor sisaldab kulda 0,000 000 5%.
0,000 000 5% = % - Elavhõbedamaaki leidub maakoores 0,000 007%.
0,000 007% = % - Prootoni läbimõõt on 0,000 000 000 000 015 m.
0,000 000 000 000 015 m = m
Päike tekkis 4 570 000 000 (
Päike tiirleb ümber Galaktika keskpunkti kiirusega 220 (
 Vaade Galaktikale ehk Linnuteele risti pöörlemistasandiga |
||||||
