Mõisted
Aritmeetikas on alati kindel, et 2 + 2 = 4. Kui me viskame münti, siis ei tea me ette, kumb külg jääb peale, kas „kull“ või „kiri“, seega juhuslikult võib peale jääda „kull“ ja juhuslikult võib peale jääda „kiri“.
Visates täringut ei saa me öelda, mitu silma täringul tuleb. Vibuga märklaua pihta lastes ei tea me, missugust märklaua punkti nool täpselt tabab. Sedalaadi sündmused on juhuslikud sündmused.
Juhusliku sündmuse toimumise võimalikkust iseloomustatakse selle tõenäosusega. Kui me teeme mõne katse, näiteks viskame mündiga „kulli ja kirja“, siis ei pruugi ilmneda mingit seaduspära. Kui katsete arv on suur, märkame, et katse tulemused hakkavad jaotuma võrdselt, pooled „kullid“, pooled „kirjad“ ning me ütleme, et tõenäosusega tuleb esile „kull“ ja tõenäosusega tuleb esile „kiri“.
Tõenäosuse esitamine
Juhuslikke sündmusi tähistatakse tähtedega A, B, C jne. Juhusliku sündmuse toimumise võimalikkust iseloomustatakse selle tõenäosusega. Tõenäosust tähistatakse tähega P ja mingi sündmuse tõenäosust sümboliga P (A). Tõenäosuse tähistus P tuleneb prantsuskeelsest sõnast probabilité – tõenäosus.
Juhusliku sündmuse A tõenäosus on arv 0 ja 1 vahel:
,
mis iseloomustab selle sündmuse toimumise võimalikkust.

See, et tõenäosuse väärtus asub 0 ja 1 vahel, tuleneb sündmuse tõenäosuse seosest selle sündmuse suhtelise sagedusega katsete seerias.
Oletame, et tehakse järjest sõltumatuid katseid ning iga kord võib meid huvitav sündmus toimuda või mitte toimuda. Kui tehakse n katset ja sündmus toimub k katsel, siis sündmuse suhteline sagedus on . On täiesti selge, et . Katsete arvu n suurenemisel hakkab suhteline sagedus lähenema kindlale arvule, mis ongi selle sündmuse tõenäosus. Kuna reaalselt on võimalik teha vaid lõplik arv katseid, siis suhtelise sageduse väärtust suure katsete arvu n korral nimetatakse ka statistiliseks tõenäosuseks.
Tüüpilised mõtlemisobjektid tõenäosusülesannetes
- Sündmus A – mündi viskamisel tuleb „kull“
- Sündmus B – pliiatsi võtmine karbist, kus on võrdselt teritamata ja teritatud pliiatseid
- Sündmus C – täringuks on kuup, veeretamisel tuleb 2 silma
- Sündmus D – täringuks on dodekaeeder, veeretamisel tuleb 2 silma
- Sündmus E – kaardipakis on 36 kaardist
veerand sinised, võetakse mittesinine kaart
Elementaarsündmus
Konkreetne sündmus on seotud nähtuse või protsessiga, millel on lõplik või lõpmatu arv üksteist välistavaid võimalikke lõpptulemusi, mida nimetatakse elementaarsündmusteks. Klassikalise tõenäosuse puhul vaadeldakse nähtusi, millel on lõplik arv n võrdvõimalikke elementaarsündmusi. Arvu n nimetatakse kõigi võimaluste arvuks. Nende elementaarsündmuste arvu k, mille korral sündmus toimub, nimetatakse soodsate võimaluste arvuks.
Märka
Kaks sündmust on teineteist välistavad, kui need ei saa toimuda ühel ajal, ja mittevälistavad, kui need võivad toimuda koos.
Näide 1
- Mündi viskamisel on meil kaks teineteist välistavat elementaarsündmust. Need on „kull“ või „kiri“ sõltuvalt sellest, missugusele küljele münt langeb.
- Täringuviskel on juba kuus elementaarsündmust. Need on vastava arvu silmade, ühest kuni kuueni, ilmumine täringu ülemisele tahule. Täringuviskel toimub alati vaid üks kuuest elementaarsündmusest ja ülejäänud viis on välistatud.
Sündmuse A klassikaline tõenäosus on
,
kus n on kõigi võimaluste arv ja k on soodsate võimaluste arv.
Näide 2
Kuubikujulise täringu viskamisel on kuus elementaarsündmust. Nendeks on pärast viset ülemisele tahule ilmunud silmade arv. Seega kõigi võimaluste arv on n = 6.
Märka
Kui ühe sündmuse tõenäosus sõltub sellest, kas teine sündmus toimub või ei toimu, siis need sündmused on sõltuvad. Kui aga sündmuse tõenäosus jääb samaks vaatamata sellele, kas teine sündmus toimub või mitte, siis on need sündmused sõltumatud.
Mõtle
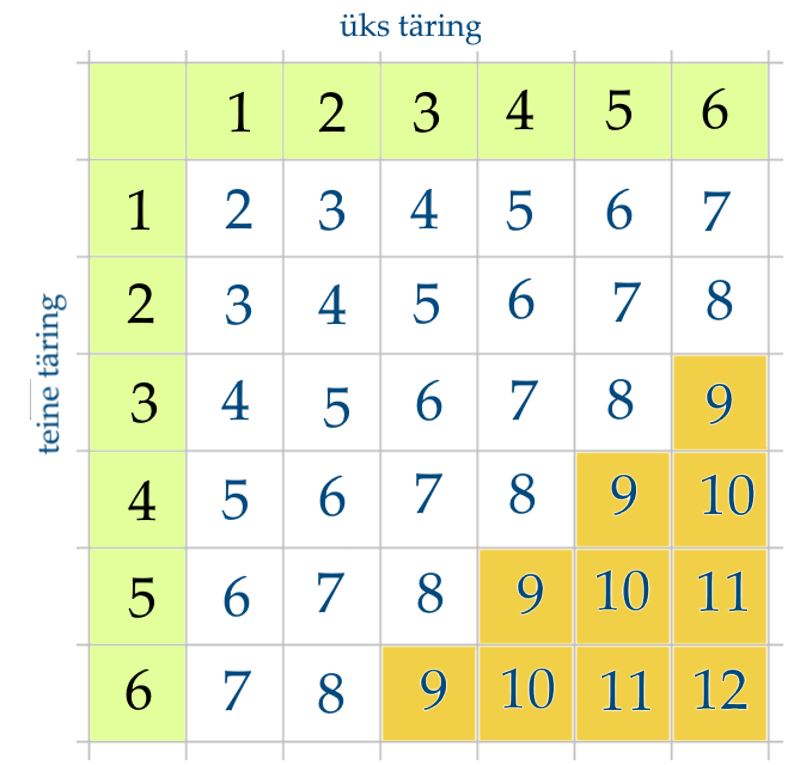
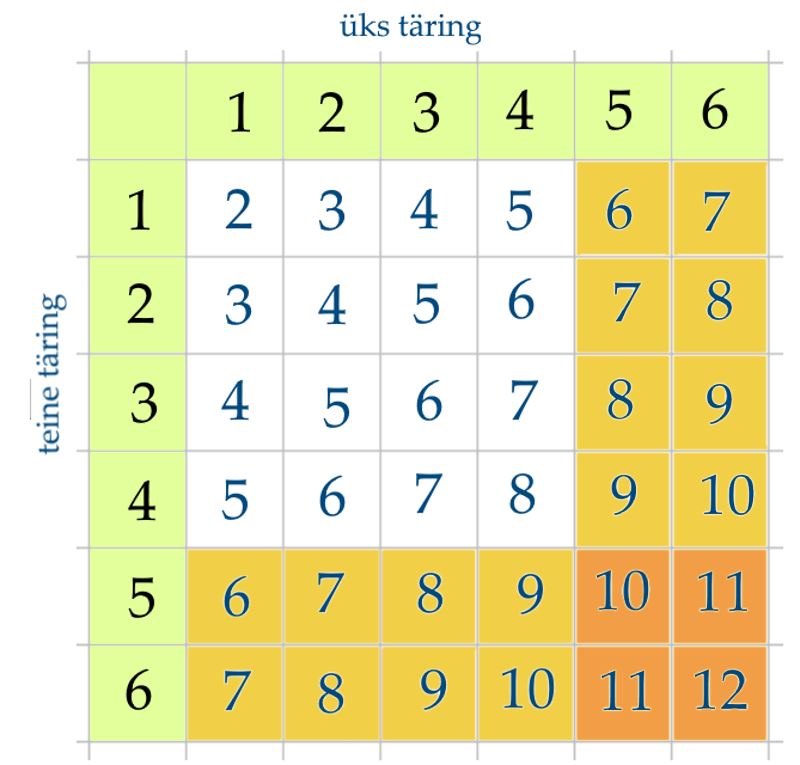
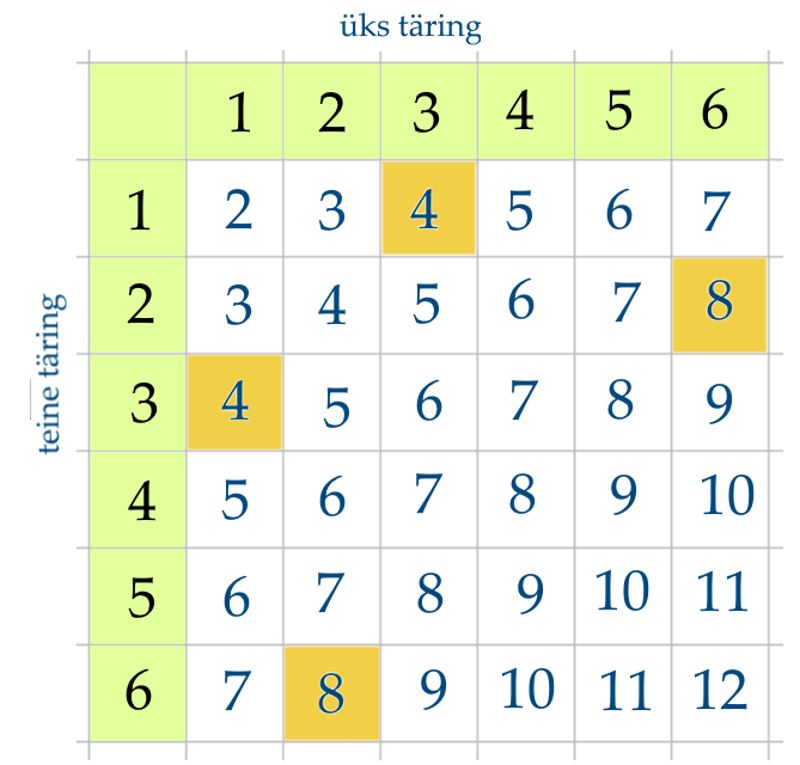
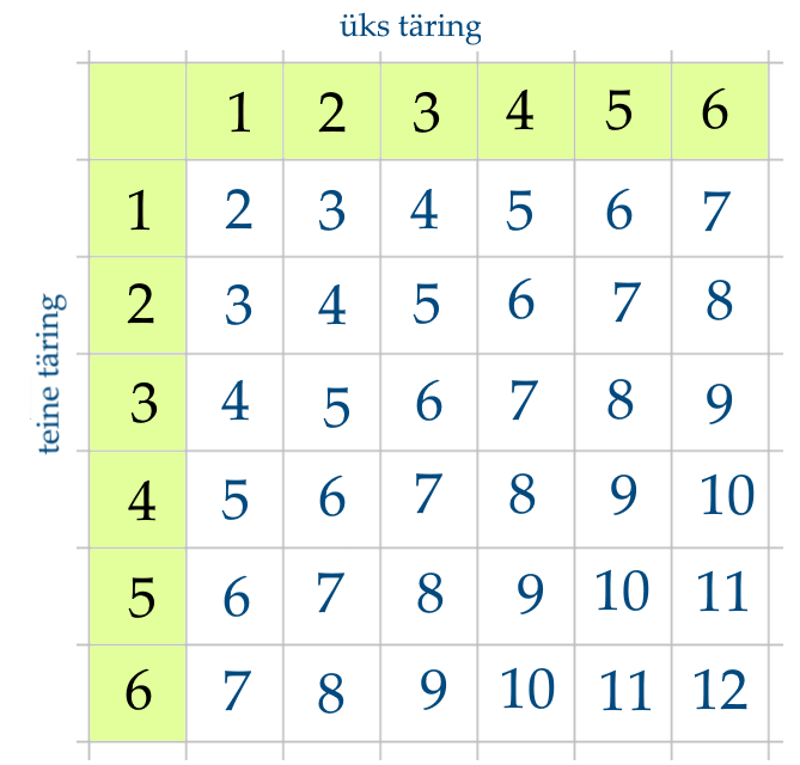
Kahe täringu viskamisel on silmade arv ühel täringul sõltumatu sellest, missugune on silmade arv teisel täringul. Seega, igale silmade arvule esimesel täringul võib kaasneda mis tahes kuuest silmade arvust teisel. Järelikult on meil n = 6 ⋅ 6 = 36 elementaarsündmust kahe täringu jaoks.
Esita vastus taandumatu murruna (va esimene slaid).
Kahe täringu viskamine. Proovi ise
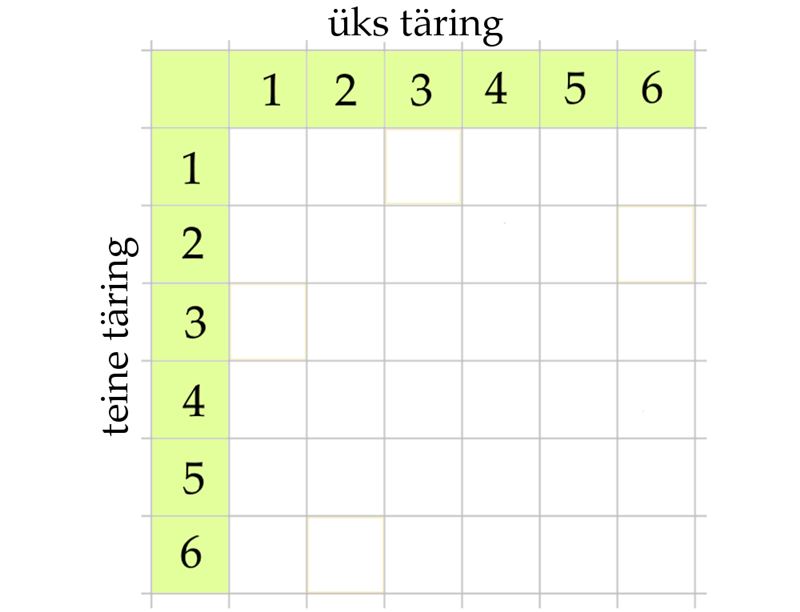
Harjuta ja treeni
Milline on tõenäosus, et see pall on
- sinine, P (A) =
- kollane, P (B) =
- punane, P (C) = ,
- sinine või kollane, P (D) = .
- poti,
P (A) = % - punast värvi mastist,
P (B) = % - pildikaart,
P (C) ≈ %, ilma ässata - kordarvulise numbriga kaart,
P (D) ≈ % - soldat,
P (E) ≈ % - risti äss
P (F) ≈ %
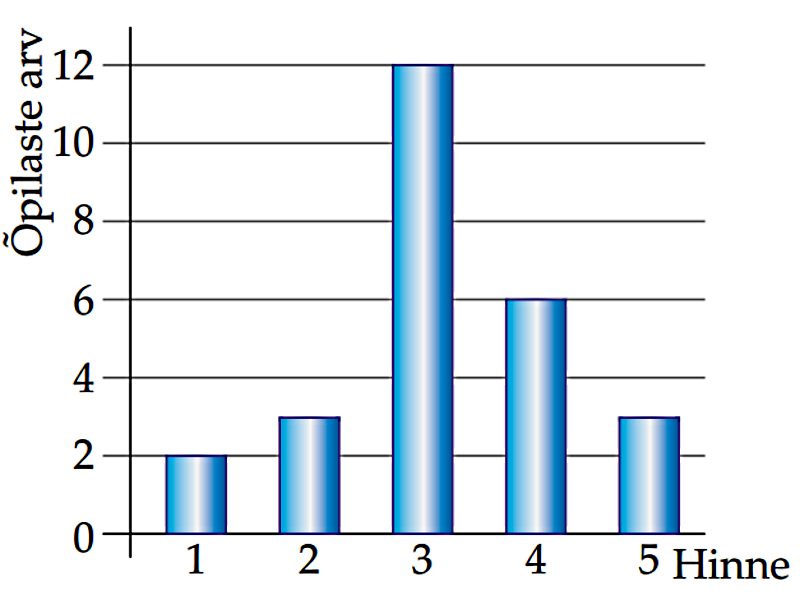
Õpetaja võtab ühe töö. Milline on tõenäosus tuhandiku täpsusega, et
- töö on sooritatud,
P (B) ≈ , - tuleb teha kordustöö,
P (C) ≈ , - töö hinne on suurem kontrolltöö keskmisest hindest ?
P (D) ≈