Изучив материал этой главы, ты
- будешь знать следующие понятия:
квадратный корень из числа, квадратное уравнение, полное квадратное уравнение, неполное квадратное уравнение, приведенное квадратное уравнение, неприведенное квадратное уравнение, дискриминант квадратного уравнения, квадратичный член, линейный член, свободный член;
- будешь знать следующие свойства понятий и соотношения между понятиями:
- соотношение между квадратным корнем из квадрата числа и модулем этого числа;
- квадратный корень из произведения;
- квадратный корень из дроби;
- формулу корней квадратного уравнения;
- теорему Виета;
- научишься:
- находить квадратный корень из числа устно или с помощью калькулятора;
- находить квадратный корень из произведения и дроби;
- решать квадратные уравнения и использовать их при решении текстовых задач;
- пользоваться дискриминантом квадратного уравнения, а также теоремой Виета при исследовании решений этого уравнения.
Квадрат числа (повторение)
Мы знаем, что произведение двух равных множителей а · а называется квадратом числа а и обозначается короче: a · a = a2. Если a = 0, то a2 = 0, так как 0 · 0 = 0. Если a ≠ 0, то a2 > 0, поскольку произведение двух положительных, как и произведение двух отрицательных чисел, всегда положительно.

Квадрат любого рационального числа неотрицателен.
 |
||||||||
52 = 5 · 5 = 25
(–1,4)2 = (–1,4) · (–1,4) = 1,4 · 1,4 = 1,96
Квадрат числа всегда можно найти с помощью умножения по образцу примера 1. При изучении следующих тем полезно запомнить таблицу квадратов чисел от 1 до 20 (она приведена в конце учебника).
Квадрат числа легко найти и с помощью калькулятора. Обычно на калькуляторе есть для этого специальная клавиша x2 и, например, квадрат числа 1,35 вычисляется по схеме: 1,35 x2.
На экране появится ответ: 1,8225.
На некоторых калькуляторах перед нажатием клавиши возведения в квадрат нужно нажать еще на клавишу 2nd.
Если на калькуляторе нет клавиши x2, то вычисление производят по схеме: 1,35 × =.
 |
||||||||
Найдем 0,242 = 0,0576 по схеме 0,24 × = или же по схеме 0,24 x2.
Аналогично: (–1,7)2 = 2,89 по схеме 1,7 × = или по схеме 1,7 x2, –2,32 = –5,29 вычислим по схеме 2,3 × = +/– или по схеме 2,3 x2 +/–.
Упражнения A
 |
||||||||
Изучи таблицу квадратов чисел 1–20 в конце учебника.
- Какими цифрами оканчиваются квадраты чисел 1–20? Какими цифрами вообще могут оканчиваться записи квадратов натуральных чисел, квадратов целых чисел? От чего зависит последняя цифра квадрата этих чисел?
- Определи, какие из следующих чисел наверняка не являются квадратом целого числа. Отметь эти числа.
- 345 743
- 61 009
- 345 744
- 259 002
- 251 000
- 361 000
- 14 641
- 6477
- 10 201
- 11 236
(ab)n = an ⋅ bn
a2 − b2 = (a −b)(a + b)
= =
= =
= =
= =
- Найди по этому правилу
252 =
552 =
1,52 =
852 =
- Квадратом какого числа является число
4225? | Это квадрат числа . |
2025? | Это квадрат числа . |
12,25? | Это квадрат числа . |
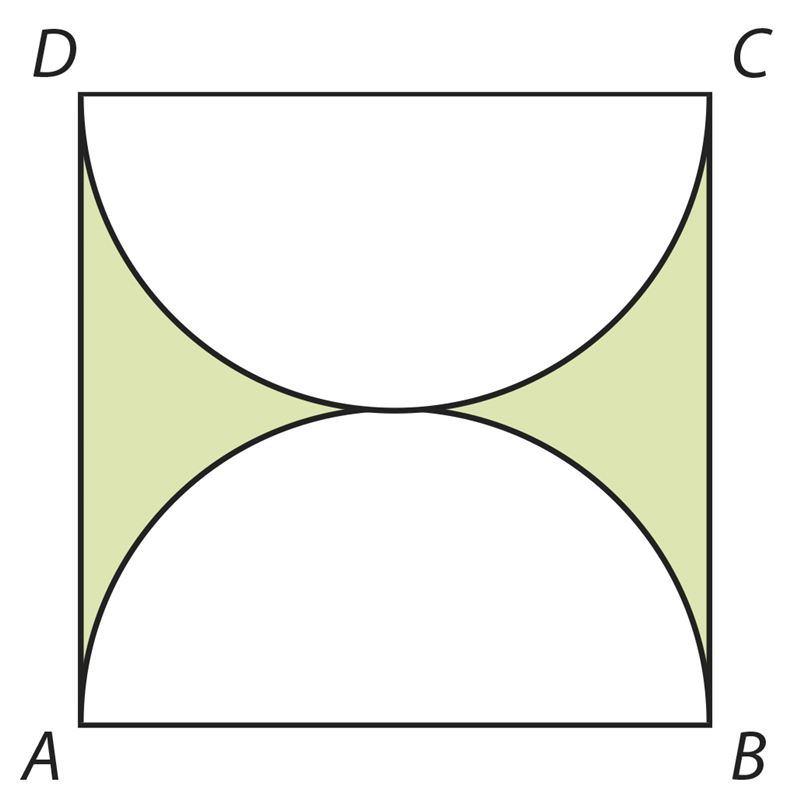
Ответ: площадь закрашенной части составляет примерно% от всей площади квадрата.
Упражнения Б
 |
||||||||
- a4b4 + 4a3b3c + 4a2b2c =
Если a = 2,4; b = 1,6; c = 2, то значение выражения приблизительно равно . - a2c2 – 2a3b2c2 + a4b4 =
Если a = 14,6; b = 2,6; c = 9,4, то значение выражения приблизительно равно . - (a2b + b2c)(a2b – b2c) =
Если a = 14,6; b = 0,8; c = 5,2, то значение выражения приблизительно равно .
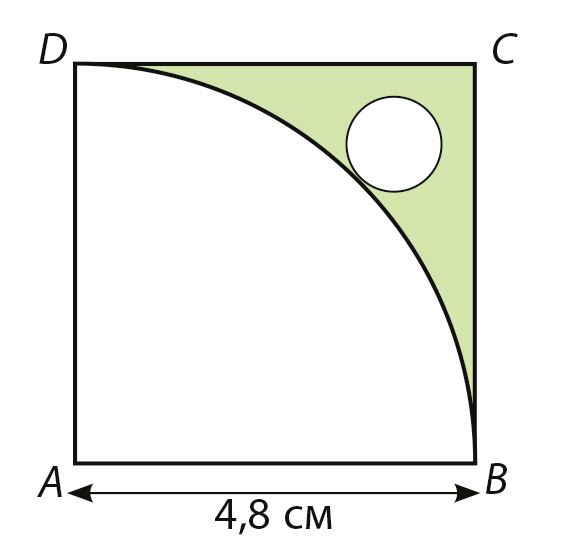
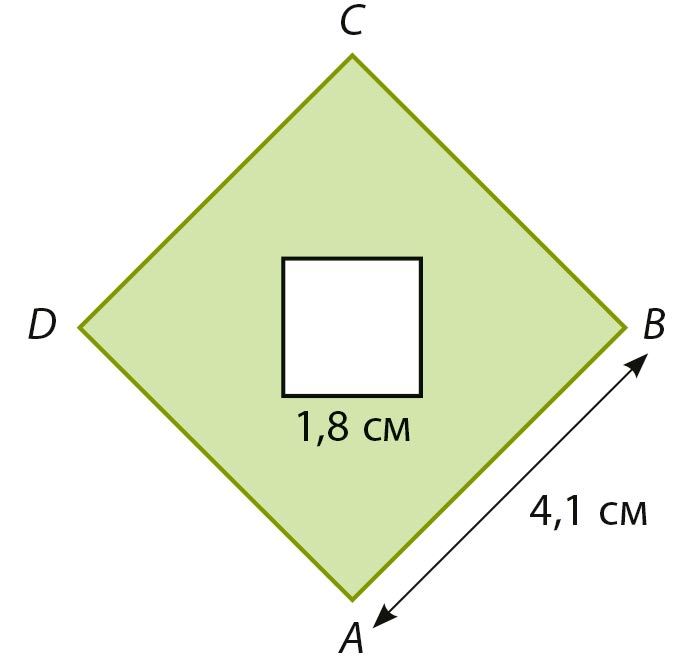
Ответ: S ≈ см2
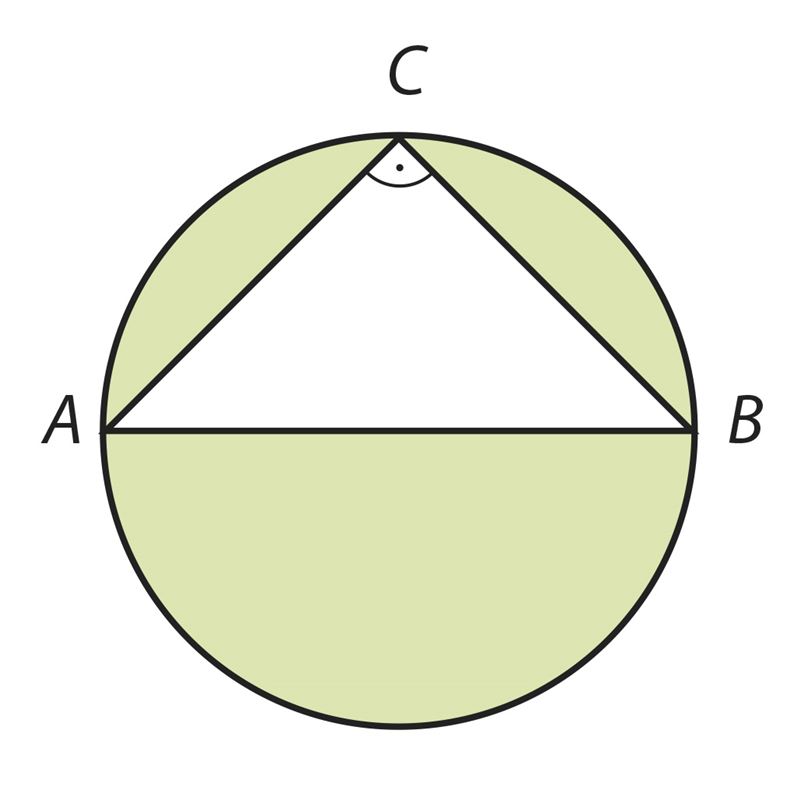
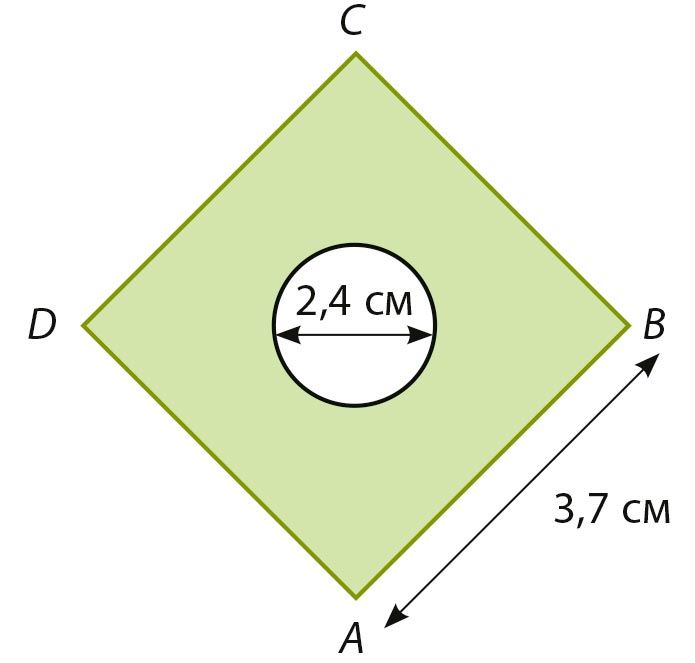
Ответ: S ≈ см2
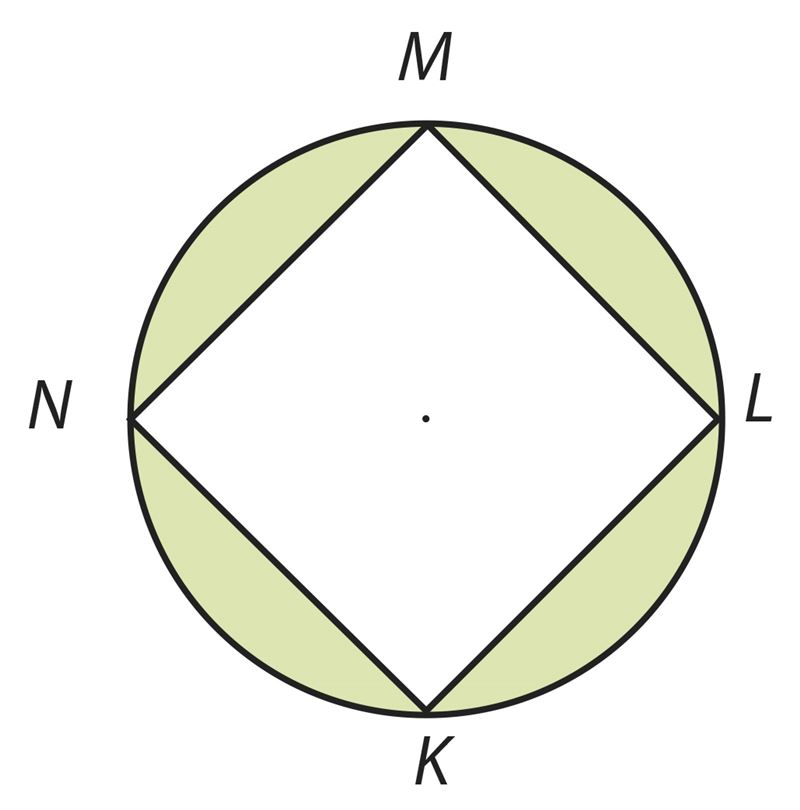
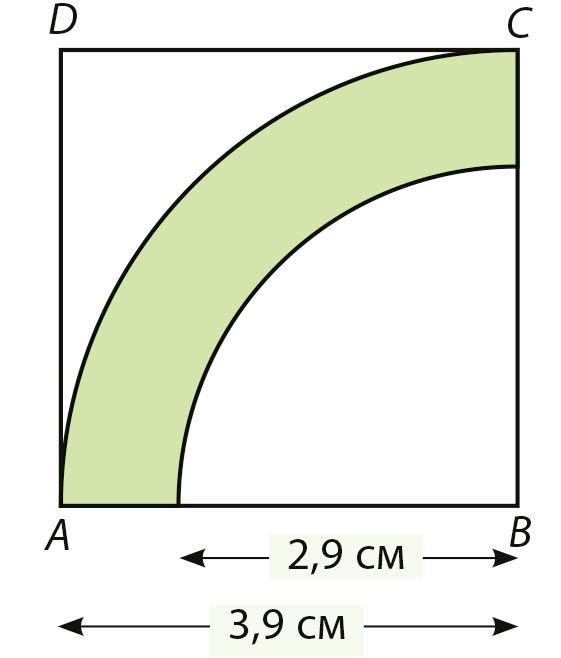
Ответ: S ≈ см2