Naturaal-, täis- ja ratsionaalarvud

Arvu mõiste hakkas kujunema aastatuhandeid tagasi, täiustudes ja üldistudes koos inimkonna arenguga. Juba ürgühiskonnas tekkis vajadus teatavaid hulki võrrelda, selleks aga tuli nende hulkade elemente loendada. Nii tekkis meile kooliõpingutest esimesena tuntuks saanud naturaalarvude hulk N[joonealune: Üldise naturaalarvude teooria üheks väljaarendajaks oli itaalia matemaatika G. Peano (1858–1932).]:

N = {0; 1; 2; 3; ...}.

Et loendamise teel on nulli raske saada, siis ei kuulunud see arv esialgu tuntud arvude hulka[joonealune: Ka tänapäeval antakse välja õpikuid ja teisi matemaatika raamatuid, kus nulli ei loeta naturaalarvuks.]. Alles 7. sajandil sõnastasid india matemaatikud reeglid arvu 0 kasutamiseks.

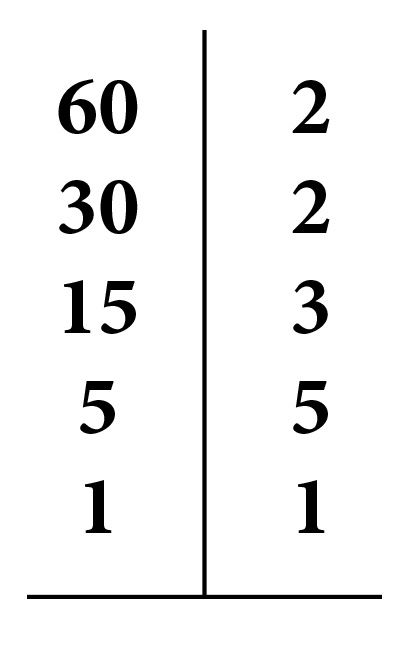
Oleme õppinud nelja põhitehet[mõiste: Põhitehted naturaalarvudega – liitmine ja korrutamine ning nende pöördtehted lahutamine ja jagamine.] naturaalarvudega[mõiste: Naturaalarv – üks arvudest 0; 1; 2; 3; ...]. Need on liitmine ja korrutamine ning nende pöördtehted lahutamine ja jagamine.

Ülesanne 1. Naturaalarvud

Nr.	a	b	a + b	a · b	a – b	a : b
1.	3	7	10	21	–4	\frac{3}{7}
2.
3.
4.
5.
6.

Eelmises ülesandes selgus, et vahe 3 – 7 ei ole naturaalarv. Seega, tundes vaid naturaalarve, ei saa me alati lahutamistehet sooritada. Siit ka vajadus laiendada uute arvudega nii, et saadud arvuhulgas oleks alati võimalik ka lahutamistehe. Võttes kasutusele naturaalarvude vastandarvud, osutubki see võimalikuks.

Naturaalarvu n vastandarv[mõiste: Vastandarv – arv, mis erineb antud arvust ainult märgi poolest. Arvu ja selle vastandarvu summa on alati 0.] –n defineeritakse selliselt, etn + (–n) = 0.

Naturaalarvud koos oma vastandarvudega moodustavad täisarvude[mõiste: Täisarvude hulk – 𝐙 = { …; –3; –2; –1; 0; 1; 2; 3; ... }] hulga Z:Z = {...; – 2; –1; 0; 1; 2; ...}.

Eraldi räägitakse veel Z⁺:Z⁺ = {1; 2; 3; ...}ja Z^–:Z^– = {...; –3; –2; –1}.

NiisiisZ = Z^– ∪ {0} ∪ Z⁺ ja N ⊂ Z .

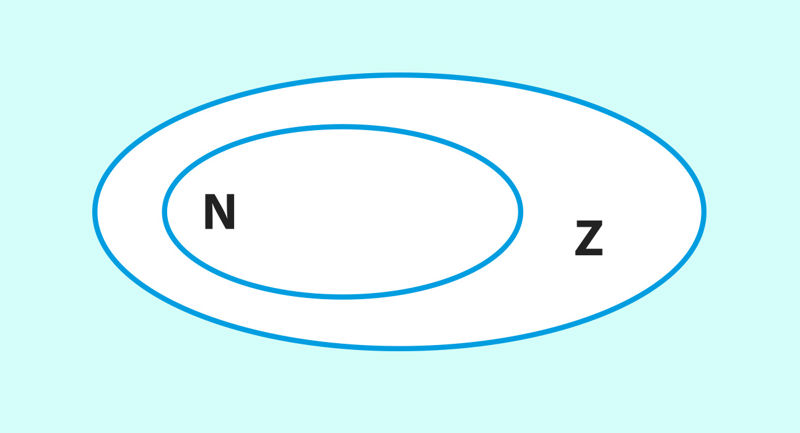Joon. 1.1

Võtnud kasutusele vastandarvud, saame tõlgendada liitmisena (vahet summana):a – b = a + (–b).

Et igal täisarvul leidub vastandarv, siis on lahutamistehe täisarvude hulgas alati võimalik – iga kahe täisarvu vahe on alati täisarv[mõiste: Täisarv – üks arvudest ..., –2, –1, 0, 1, 2, ...].Täisarvud liigituvad paaris- ja paarituteks arvudeks. Täisarvu, mis jagub kahega, nimetatakse paarisarvuks[mõiste: Paarisarv – täisarv, mis jagub kahega.]. Ta on esitatav kujul 2n, kus n ∈ Z. Paaritud[mõiste: Paaritu arv – täisarv, mis ei jagu kahega.], s.t kahega mittejaguvad täisarvud, esituvad aga kujul 2n + 1, kus n ∈ Z.

Ülesanne 2. Täisarvud

Nr.	a	b	a + b	a · b	a – b	a : b
1.	3	7	10	21	–4	\frac{3}{7}
2.
3.
4.
5.
6.

Äsja lahendatud ülesandes selgus, et täisarvude jagatis pole alati täisarv. Kui arv a jagub arvuga b (b ≠ 0), siis on jagatiseks täisarv, vastasel juhul murdarv[mõiste: Murdarv – reaalarv, mis pole täisarv.]

\frac{a}{b}

. Kui a ja b on samamärgilised, siis on see murd , kui erimärgilised, siis .

Laiendades täisarvude hulka murdarvudega, saame uue arvuhulga, kus on alati võimalik ka jagamistehe (v.a jagamine nulliga). Kõik täisarvud ning positiivsed ja negatiivsed murdarvud kokku moodustavad ratsionaalarvude[mõiste: Ratsionaalarvude hulk – 𝐐 = {...; –54,(1); ...; –7; ...; 0; ...; 5,17; ...; 111; ...}] hulga Q. (joon. 1.2).

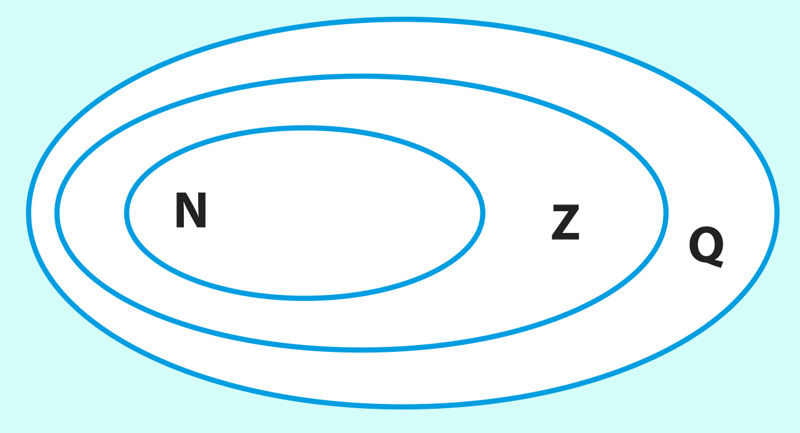
Joon. 1.2

Kuna iga täisarvu saab avaldada jagatisena \frac{a}{b} (näiteks -5=-\frac{10}{2}; 0=\frac{0}{2}), siis võime defineerida, et

ratsionaalarvuks[mõiste: Ratsionaalarv – arv, mis avaldub kahe täisarvu jagatisena, kusjuures jagaja ei tohi olla null. Iga ratsionaalarvu saab esitada ka kas lõpliku või lõpmatu perioodilise kümnendmurruna.] nimetatakse arvu, mis avaldub jagatisena $\frac{a}{b}$ , kus a ∈ Z, b ∈ Z ja b ≠ 0.

Murdudega seoses oleme kasutanud veel järgmisi mõisteid:

harilik murd[mõiste: Harilik murd – murdarv, mis on kirjutatud kahe naturaalarvu ja murrujoone abil.]: $\frac{a}{b}$ (a ∈ N, b ∈ N ja b ≠ 0),

lihtmurd[mõiste: Lihtmurd – harilik murd, mille lugeja on nimetajast väiksem.]: $\frac{a}{b}$ (a ∈ N, b ∈ N, b ≠ 0 ja a < b),

liigmurd[mõiste: Liigmurd – harilik murd, mille lugeja on võrdne nimetajaga või sellest suurem.]: $\frac{a}{b}$ (a ∈ N, b ∈ N, b ≠ 0 ja a ≥ b),

segaarv[mõiste: Segaarv – naturaalarvu ja lihtmurru summa, mis on kirjutatud ilma plussmärgita.]: naturaalarvu ja lihtmurru summa: 2\frac{1}{2}=2+\frac{1}{2},kümnendmurd[mõiste: Kümnendmurd – koma abil esitatud murdarv.]: murd, mis on kirjutatud koma abil, kus esimene number pärast koma tähendab kümnendikke, teine sajandikke, jne: 3,75=3+\frac{7}{10}+\frac{5}{100}.Ühte ja sama arvu võib esitada mitmel erineval kujul: 1\frac{1}{2}=\frac{3}{2}=1,5.

Iga ratsionaalarvu saab esitada kümnendmurruna, kui jagada lugeja nimetajaga. Siin esineb kaks erinevat olukorda:

Ühel juhul tekib lõplik kümnendmurd[mõiste: Lõplik kümnendmurd – kümnendmurd, milles on olemas viimane nullist erinev numbrikoht.]:

\frac{51}{40}=1,275.

Teisel juhul hakkab jagamisel mingi jääk korduma ja tekib lõpmatu perioodiline kümnendmurd[mõiste: Lõpmatu perioodiline kümnendmurd – kümnendmurd, milles viimane number või numbrirühm kordub lõputult.]:

\frac{17}{6}=17\ :\ 6=2,833...=2,8\left(3\right).Et ka lõplikku kümnendmurdu on võimalik esitada lõpmatuna ja perioodilisena (1,275 = 1,27500… = 1,275(0)), siis võime öelda:

iga ratsionaalarv avaldub lõpmatu perioodilise kümnendmurruna.

Kehtib ka vastupidine väide:

iga lõpmatu perioodiline kümnendmurd esitab ratsionaalarvu.

Näide.Avaldame lõpmatu perioodilise kümnendmurru x = 1,2(43) kahe täisarvu jagatisena.

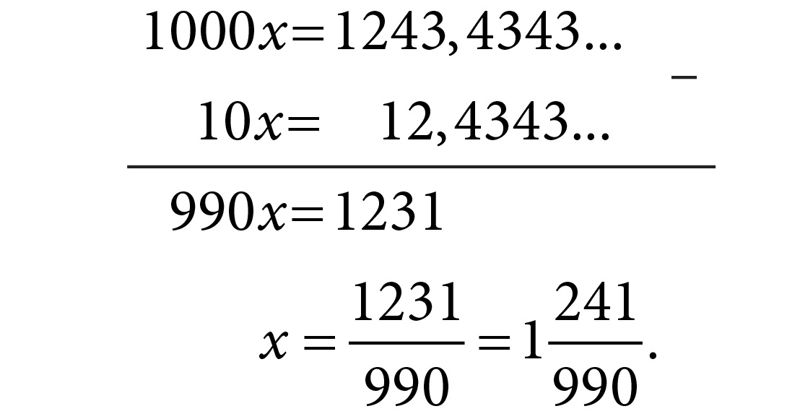a ja $\frac{1}{a}$ on teineteise pöördarvud[mõiste: Pöördarvud – kaks arvu, mille korrutis on võrdne 1-ga. Hariliku murru pöördarv leitakse murru lugeja ja nimetaja vahetamise teel.].

Seotud sisu

Ülesanded A

Ülesanne 3. Naturaal-, täis- ja ratsionaalarvud

–1,5
$12 \frac{1}{2}$
40
$- \frac{7}{5}$
21,01
$\frac{1000}{5}$
12,5
–15
$- \frac{2}{3}$
$\frac{4}{7}$
15
0
–40
2,3
0,005

–1,5
$12 \frac{1}{2}$
40
$- \frac{7}{5}$
21,01
$\frac{1000}{5}$
12,5
–15
$- \frac{2}{3}$
$\frac{4}{7}$
15
0
–40
2,3
0,005

–1,5
$12 \frac{1}{2}$
40
$- \frac{7}{5}$
21,01
$\frac{1000}{5}$
12,5
–15
$- \frac{2}{3}$
$\frac{4}{7}$
15
0
–40
2,3
0,005

–1,5
$12 \frac{1}{2}$
40
$- \frac{7}{5}$
21,01
$\frac{1000}{5}$
12,5
–15
$- \frac{2}{3}$
$\frac{4}{7}$
15
0
–40
2,3
0,005

–1,5
$12 \frac{1}{2}$
40
$- \frac{7}{5}$
21,01
$\frac{1000}{5}$
12,5
–15
$- \frac{2}{3}$
$\frac{4}{7}$
15
0
–40
2,3
0,005

–1,5
$12 \frac{1}{2}$
40
$- \frac{7}{5}$
21,01
$\frac{1000}{5}$
12,5
–15
$- \frac{2}{3}$
$\frac{4}{7}$
15
0
–40
2,3
0,005

–1,5
$12 \frac{1}{2}$
40
$- \frac{7}{5}$
21,01
$\frac{1000}{5}$
12,5
–15
$- \frac{2}{3}$
$\frac{4}{7}$
15
0
–40
2,3
0,005

–1,5
$12 \frac{1}{2}$
40
$- \frac{7}{5}$
21,01
$\frac{1000}{5}$
12,5
–15
$- \frac{2}{3}$
$\frac{4}{7}$
15
0
–40
2,3
0,005

–1,5
$12 \frac{1}{2}$
40
$- \frac{7}{5}$
21,01
$\frac{1000}{5}$
12,5
–15
$- \frac{2}{3}$
$\frac{4}{7}$
15
0
–40
2,3
0,005

–1,5
$12 \frac{1}{2}$
40
$- \frac{7}{5}$
21,01
$\frac{1000}{5}$
12,5
–15
$- \frac{2}{3}$
$\frac{4}{7}$
15
0
–40
2,3
0,005

Ülesanne 4. Murrud

–1,5
$12 \frac{1}{2}$
40
$- \frac{7}{5}$
21,01
$\frac{1000}{5}$
12,5
–15
$- \frac{2}{3}$
$\frac{4}{7}$
15
0
–40
2,3
0,005

–1,5
$12 \frac{1}{2}$
40
$- \frac{7}{5}$
21,01
$\frac{1000}{5}$
12,5
–15
$- \frac{2}{3}$
$\frac{4}{7}$
15
0
–40
2,3
0,005

–1,5
$12 \frac{1}{2}$
40
$- \frac{7}{5}$
21,01
$\frac{1000}{5}$
12,5
–15
$- \frac{2}{3}$
$\frac{4}{7}$
15
0
–40
2,3
0,005

–1,5
$12 \frac{1}{2}$
40
$- \frac{7}{5}$
21,01
$\frac{1000}{5}$
12,5
–15
$- \frac{2}{3}$
$\frac{4}{7}$
15
0
–40
2,3
0,005

Ülesanne 5. Naturaal-, täis- ja ratsionaalarvud

naturaalarvud;
täisarvud ega harilikud murrud;
täisarvud;
naturaalarvud ega kümnendmurrud.

Ülesanne 6. Naturaal-, täis- ja ratsionaalarvud

ei ole täisarvud;
ei ole positiivsed täisarvud;
on ratsionaalarvud;
on täisarvud.

Ülesanne 7. Naturaal-, täis- ja ratsionaalarvud

Iga naturaalarv on täisarv.
Iga ratsionaalarv on täisarv.
Iga täisarv pole ratsionaalarv.
Iga naturaalarv on positiivne.
Leidub ratsionaalarve, mis pole täisarvud.
Leidub naturaalarve, mis pole ratsionaalarvud.
Leidub täisarve, mis on naturaalarvud.
Leidub naturaalarv, mis pole positiivne.
Iga harilik murd on täisarv.
Iga naturaalarv on esitatav hariliku murruna.
Leidub harilikke murde, mis on täisarvud.
Leidub lihtmurd, mis on naturaalarv.

Ülesanne 8. Vastandarvud ja pöördarvud

Vastus. Arvude 7 ja –13 summa vastandarv on .

Vastus. Arvude 7 ja –13 vastandarvude vahe on .

Vastus. Arvude 7 ja –13 vahe pöördarv on .

Vastus. Arvude 7 ja –13 pöördarvude summa on .

Vastus. Arvude 7 ja –13 pöördarvude vahe ja vastandarvude summa jagatis on .

Vastus. Arvude 7 ja –13 vastandarvude summa ja pöördarvude vahe korrutis on .

Ülesanne 9. Hariliku murru avaldamine kümnendmurruna

\frac{7}{16}

$\frac{81}{80}$ =

$- \frac{9}{25}$ =

$\frac{7}{9}$ =

$\frac{2}{3}$ =

$- \frac{5}{18}$ =

Ülesanne 10. Kümnendmurru avaldamine kahe täisarvu jagatisena

0,(5) =

1,34(5) =

0,4(12) =

0,(9) =

1,(4) =

0,7(5) =

2,2(34) =

3,(9) =

Seotud sisu

Ülesanded B

Ülesanne 11. Lõplik kümnendmurd või lõpmatu kümnendmurd?

\frac{7}{16}

\frac{81}{80}

-\frac{9}{25}

\frac{7}{9}

\frac{2}{3}

-\frac{5}{18}

Milliste murdude nimetajate algteguriteks on vaid arvude 2 ja 5 astmed?
Millised taandumatud murrud teisenevad lõplikuks kümnendmurruks, millised mitte?

Põhjendage punktis 2 püstitatud hüpotees. Uurige selleks järgnevat näidet:
\frac{3}{40}=\frac{3}{2\cdot2\cdot2\cdot5}=\frac{3\cdot5\cdot5}{2\cdot5\cdot2\cdot5\cdot2\cdot5}=\frac{75}{1000}=0,075

Ülesanne 12. Kümnendmurru avaldamine kahe täisarvu jagatisena

0,(7) = ;

0,(76) = ja

0,(765) = .

Sõnastage reegel analoogiliste lõpmatute perioodiliste kümnendmurdude teisendamiseks harilikeks murdudeks.

Ülesanne 13. Kümnendmurru avaldamine kahe täisarvu jagatisena

0,2(5) = ;

0,2(54) = ;

0,2(543) = ja

0,12(54) = .

Sõnastage reegel analoogiliste kümnendmurdude teisendamiseks harilikeks murdudeks.

Seotud sisu

Opiqus edenemine

	Tööd
	Peatükk on läbi töötatud

Naturaal-, täis- ja ratsionaal­arvud

Ülesanne 1. Naturaal­arvud

Ülesanne 2. Täis­arvud

Seotud sisu

Ülesanded A

Ülesanne 3. Naturaal-, täis- ja ratsionaal­arvud

Ülesanne 4. Murrud

Ülesanne 5. Naturaal-, täis- ja ratsionaal­arvud

Ülesanne 6. Naturaal-, täis- ja ratsionaal­arvud

Ülesanne 7. Naturaal-, täis- ja ratsionaal­arvud

Ülesanne 8. Vastand­arvud ja pöörd­arvud

Ülesanne 9. Hariliku murru avaldamine kümnend­murruna

Ülesanne 10. Kümnend­murru avaldamine kahe täis­arvu jagatisena

Seotud sisu

Ülesanded B

Ülesanne 11. Lõplik kümnend­murd või lõpmatu kümnend­murd?

Ülesanne 12. Kümnend­murru avaldamine kahe täis­arvu jagatisena

Ülesanne 13. Kümnend­murru avaldamine kahe täis­arvu jagatisena

Seotud sisu

Lisa materjali

Lisatavad failid

Teata veast

Teata siia ainult Opiqu veast. Palun kirjelda viga nii täpselt kui võimalik.

Kui ootad Opiqu meeskonnalt vastust, lisa oma kontaktandmed (e-post, telefon).

Tee linnuke, et aidata meil spämmiga võidelda

Opiq kasutab küpsiseid

Naturaal-, täis- ja ratsionaalarvud

Ülesanne 1. Naturaalarvud

Ülesanne 2. Täisarvud

Ülesanne 3. Naturaal-, täis- ja ratsionaalarvud

Ülesanne 5. Naturaal-, täis- ja ratsionaalarvud

Ülesanne 6. Naturaal-, täis- ja ratsionaalarvud

Ülesanne 7. Naturaal-, täis- ja ratsionaalarvud

Ülesanne 8. Vastandarvud ja pöördarvud

Ülesanne 9. Hariliku murru avaldamine kümnendmurruna

Ülesanne 10. Kümnendmurru avaldamine kahe täisarvu jagatisena

Ülesanne 11. Lõplik kümnendmurd või lõpmatu kümnendmurd?

Ülesanne 12. Kümnendmurru avaldamine kahe täisarvu jagatisena

Ülesanne 13. Kümnendmurru avaldamine kahe täisarvu jagatisena