Tunni ülesehitus
- Sissejuhatus, 12 min
- Naturaalarvude ümardamine, 20 min
- Kinnistamine, 10 min
- Kokkuvõte, 3 min
Ettevalmistus
Printida sedelid õpilaste paaridesse jagamiseks.
Eelteadmised
Õpilane
- tunneb võrratusmärke ja nende tähendust;
- kujutab naturaalarve arvkiirel;
- võrdleb naturaalarve.
Eesmärgid
Õpilane
- tunneb ligikaudse võrduse märki;
- selgitab ümardamise, ligikaudse võrduse, lähima täiskümne ja lähima täissaja mõistet;
- määrab arvu lähimat täiskümmet ja lähimat täissadat;
- ümardab naturaalarve mis tahes järguni.
Seotud materjal
- ptk 2.5 „Naturaalarvude ümardamine“
- lk 16–18
- lk 8
Märksõnad ja meetodid
- Ümardamine, lähim täiskümme, lähim täissada, ligikaudselt võrdne, ligikaudse võrduse märk, arvu järk
- Vestlus, arvude meeldejätmine, arutelu, animatsioon, iseseisev töö, paaristöö
Lõiming
- Matemaatika 4. kl (Arvkiir. Arvu järgud)
Läbivad teemad
- Elukestev õpe ja karjääri planeerimine
- Tehnoloogia ja innovatsioon
1. Sissejuhatus
12
- Kodutöö (TV lk 6, 7) kontrollimine
- Arvude meeldejätmine
- Ümardamise vajadusest
- Näiteid ligikaudsete arvude kohta
- Arutelu
- Tunni teema
Soovi korral kontrollitakse tunni alguses ära kodutöö vastused.
Seejärel näitab õpetaja ekraanil slaide arvudega ja palub õpilastel arvud meelde jätta.
Õpetaja hoiab slaidi mõne hetke ekraanil ja küsib siis õpilastelt, mis arvud slaidil olid.
Tõenäoliselt jäävad need arvud õpilastele lihtsasti meelde ja nad suudavad hetke pärast öelda, mis arve nad nägid.
Nüüd kuvab õpetaja ekraanil uue slaidi arvudega ja palub õpilastel jälle arvud meelde jätta.
Õpetaja hoiab slaidi mõne hetke ekraanil ja küsib siis õpilastelt, mis arvud slaidil olid.
Tõenäoliselt on neid arve raskem meelde jätta kui eelmisi ja osa õpilasi ei suuda kõiki arve õigesti nimetada.
Nüüd kuvab õpetaja ekraanil veel ühe slaidi arvudega ja palub jälle õpilastel arvud meelde jätta.
Õpetaja hoiab slaidi mõne hetke ekraanil ja küsib siis õpilastelt, mis arvud slaidil olid.
Tõenäoliselt ei suuda suurem osa õpilastest slaidil olnud arve täielikult meenutada.
Sellest järeldatakse, et mida rohkem on arvus nullist erinevaid numbreid, seda raskem on arvu meelde jätta. Suuri arve on kergem meeles pidada, kui arvus on vähem nullist erinevaid numbreid, seepärast arve sageli ümardatakse.
Vahel ümardatakse arvandmeid seetõttu, et need muutuvad kiiresti ja arvu väiksematel järkudel (nt ühelistel ja kümnelistel) ei ole igapäevaelus suurt tähtsust. Õpetaja toob näiteks elanike arvu riigis. Selleks saab kasutada veebilehte, mis näitab elanikke arvu reaalajas. Saame teada, et Eestis elab ligikaudu 1 300 000 püsielanikku. Klikkides pealkirja all oleval lingil „World Population“, saab õpilastele näidata, kui palju elanikke on terves maailmas. Arvu üheliste number muutub pidevalt, sest iga hetk keegi sünnib või sureb.
Ümardatud arve või arvandmeid kajastades kasutatakse sageli mõisteid „umbes”, „ligikaudu” või „ligikaudselt võrdne”.

Slaidil esimene arv näitab Eesti elanike arvu 2011. a rahvaloenduse põhjal, teine arv aga elanike arvu aastal 2022.
Õpetaja arutleb õpilastega, miks on mõlemad arvud ligikaudselt võrdsed arvuga 1 300 000.
Abistavad küsimused aruteluks
- Millise järguni on mõlemat arvu ümardatud? Sajatuhandelisteni
- Millised arvud moodustavad tuhandete klassi? 294 ja 326
- Milliste täissadade vahele need arvud jäävad?
200 < 294 < 300
300 > 326 < 400 - Kummale täissajale on need arvud lähemal?
294 ≈ 300 ja 326 ≈ 300
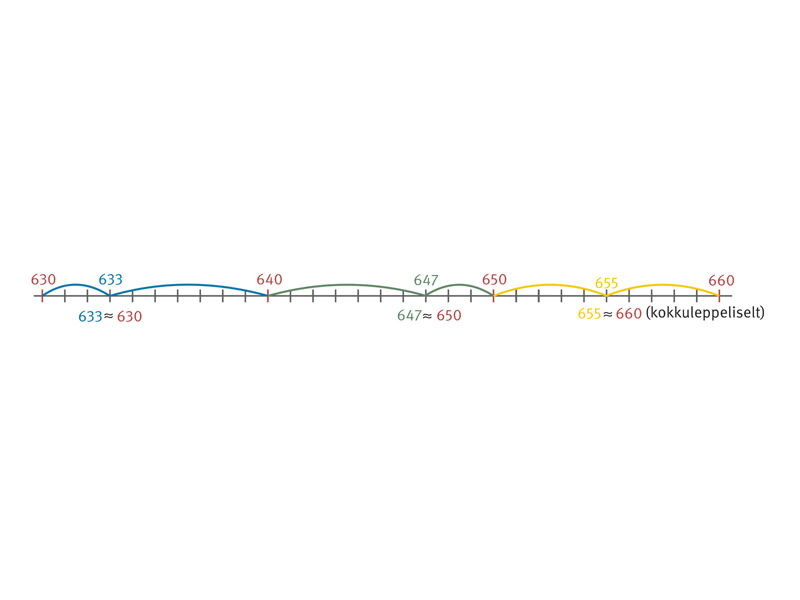
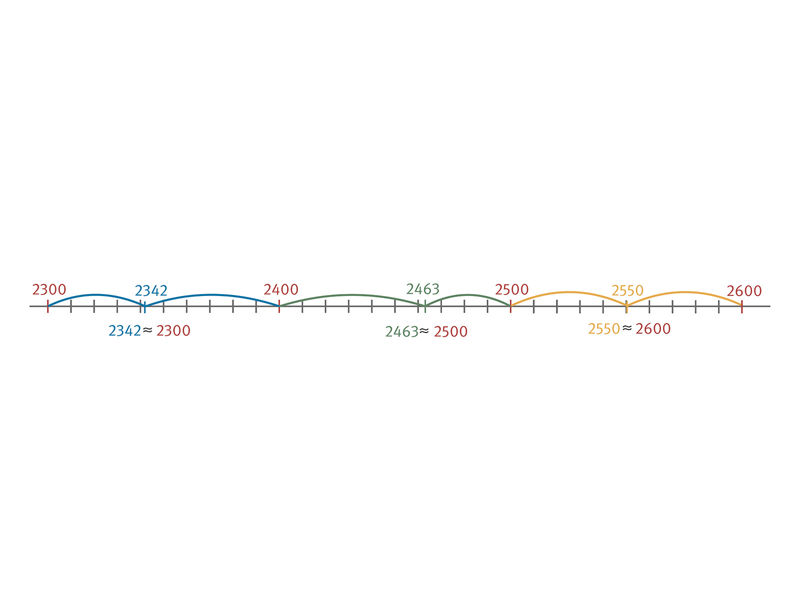
2. Naturaalarvude ümardamine
20
- Täpsemõõdu asendamine ligikaudsega, Õ ül 30, Opiq ptk 2.5
- Animatsioon
- Ümardamine kümnelisteni ja sajalisteni arvkiire abil
- Õ ül 31–32 näidete uurimine. Õ ül 34 ja 36 suuliselt, Opiq ül 2, 4
- Reeglid arvu ümardamiseks mingi järguni. Õ ül 33, Opiq ül 1
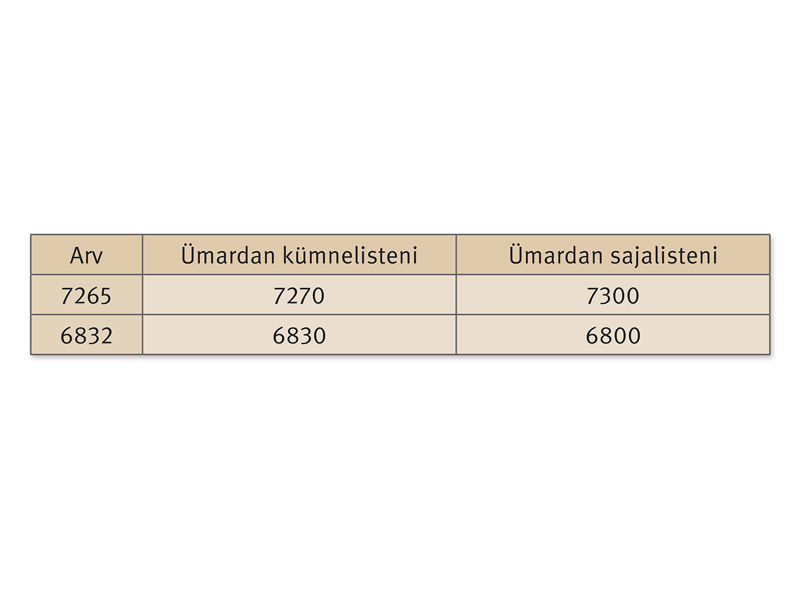
Õpilased avavad lk 16 ül 30 või ptk 2.5 ja loevad pildiallkirju ning asendavad seejärel täpse mõõdu ligikaudsega.
Õ ül 30 vastused
Kuna ülesandes pole ette antud, millise järguni tuleb ümardada, siis on õiged ka need vastused, mis ümardatakse mingi muu järguni.
- 8851 km ≈ 9000 km
- 6695 km ≈ 6700 km
- 6800 km ≈ 7000 km
- 11 022 m ≈ 11 000 m
- 1630 m ≈ 1600 m
- 8848 m ≈ 9000 m
Õpetaja näitab õpilastele animatsiooni.
Seejärel uuritakse üheskoos ül 31 ja 32 näiteid või ptk 2.5 näiteid ja lahendatakse suuliselt ül 34 ja 36 või ül 2 ja 4.
Õpetaja kuvab ekraanil reeglid ja seejärel näited, mis ühiselt läbi arutatakse. Õpilased kirjutavad näited vihikusse.
3. Kinnistamine
10
- Paarilise leidmine
- Paaristöö. TV ül 9–10
Tund jätkub paaristööga.
Paarilise leidmine
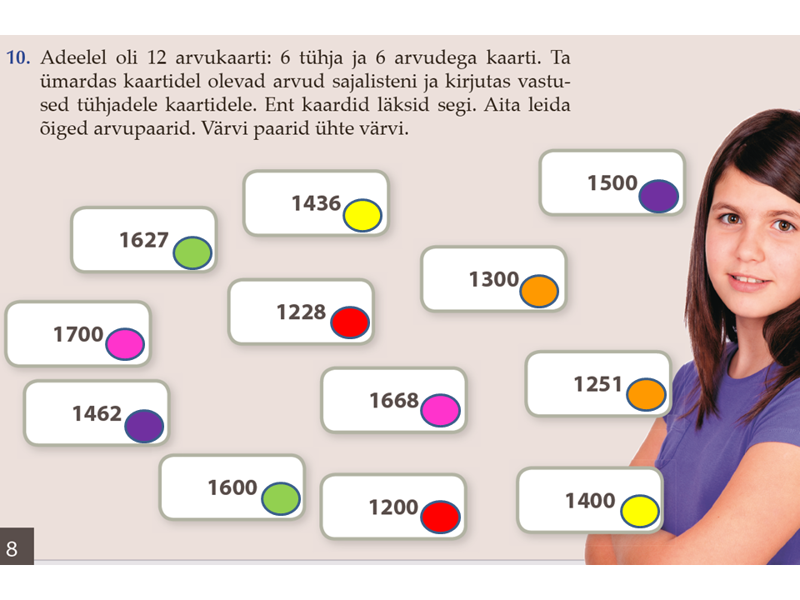
Õpilased tõmbavad loosi ja leiavad paarilise. Paari moodustavad ümardamata arv ja selle arvu kümnelisteni ümardatud arv. Kõik õpilased, kelle sedelil on ümardamata arv, kogunevad klassi ette. Kordamööda ütlevad nad oma lipikul oleva arvu. Teised õpilased vaatavad, kas nende lipikul olev arv – ümardatud kümnelisteni – sobib öeldud arvuga. Niiviisi moodustatakse paarid ning asutakse lahendama ül 9–10.
TV ül 9 vastused õpetajale
4. Kokkuvõte
3
- Peastarvutamine ja ümardamine
Tund lõpetatakse peastarvutamise ja tulemuse ümardamisega sajalisteni. Õpilased (paarid) korrutavad paaristööks tõmmatud ümardamata arvu 10-ga ja ümardavad saadud tulemuse sajalisteni.
Peastarvutamise ja ümardamise vastused õpetajale
Kui tund kulges kiiremini ja aega on piisavalt, võib õpilastelt küsida, kas nad märkasid seost sedelitel olevate arvude ja nüüd 10-ga korrutatud ja sajalisteni ümardatud arvude vahel.
Vastus. Sedelil oleva ümardatud arvu oleks võinud korrutada 10-ga.
Kodutöö ja tunni kirjeldus
Kodutöö
Tunni kirjeldus
Naturaalarvude ümardamine |
Õ lk 16–18, TV lk 8, Opiq ptk 2.5 |